reversi/othello - bitboard tricks

リバーシのビットボードテクニック

[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]

OD＞ハッカーのたのしみOD版本物のプログラマはいかにして問題を解くか [ ヘンリー・S．ウォーレン ]
価格：3,740円（税込、送料無料) (2024/1/22時点)

(†は外部サイトへのリンク)

Population count - 現時点の石数
Mirroring - 鏡像
Mobility - 着手可能位置
Get full lines - 埋まっている列を求める
Count Last Flip - 最終手での返る石数
Flip - 返る石を求める (Move Generator)
Flip AVX2 - AVX2 / AVX512 で返る石を求める
Flip Neon - Arm Neon / SVE で返る石を求める

リバーシの盤面は 8×8 の 64 マスで、石の有無をビットで表せるので、ビットボードへの納まりは非常に良い。
以下盤面の A1 を bit 0 (LSB), H8 を bit 63 (MSB) とする。（盤面とビットの並びが逆になる。）
自分の石 P と相手の石 O の 2 つの 64 ビット変数で盤面を表す。（文中で O (オー) と 0 (ゼロ) の両方が使われているので注意。）
SSE2 では 128 ビット変数 OP で表せる。以下 (Arm Neon のいくつかの例を除き) x86 (64) に特化した最適化を多く含む。
int は 32 ビット長、long long は 64 ビット長と仮定する。

隣のマスは±1、上下のマスは±8、斜めのマスは±7, ±9。本来離れている左右の辺が連続しているので、折り返し (Alias) の処理が必要なことがある。
位置 x からビットへの変換は

	1ULL << x

((unsigned long long)(1 << x) は NG)、またはテーブル参照で

	X_TO_BIT[x]

メモリアクセスが増えるが、Edax のコメントによればこの方が速いこともあるようだ。
MMX / SSE / AVX レジスターでは定数 1 のロードもメモリー参照（または PCMPEQD + PSRLQ のような複数命令）になるため、テーブル参照の方が速い。

P が x に打ち、flipped が返ると、

	P ^= (flipped | X_TO_BIT[x]);
	O ^= flipped;

flipped の求め方は Flip (Move Generator) で扱う。

NTest は盤面を石のあるビット (= P | O) と自分の石の 2 つの 64 ビット変数で表す方法を使っている。石を返す処理、手番を入れ替える処理がそれぞれ 1 ～数命令短くなる。

Population count - 現時点の石数

64 ビット中での１の数を数える、よく解説されるビット処理（分割統治, SWAR）のアルゴリズム。
SSE4.2 / AMD ABM では POPCNT 命令が追加され、一命令で高速に実行されるが、 x86-64 でも初期の CPU ではサポートされていないものもあり、その場合に必要になる。

たとえば Software Optimization Guide for the AMD64 Processors (pub.25112) の 179ページ†に解説と実装例がある。

64ビットでの実装:

	x = x - ((x >> 1) & 0x5555555555555555);
	x = (x & 0x3333333333333333) + ((x >> 2) & 0x3333333333333333);
	x = (x + (x >> 4)) & 0x0F0F0F0F0F0F0F0F;
	x = (x * 0x0101010101010101) >> 56;

32ビットCPUの場合、上位・下位ワードに分けて CPU で求めるほか、MMX で上記の実装も可能。 SSE2 では PSADBW で水平加算できるが、それでもあまり速くない。
SSSE3 では PSHUFB を使って 4 ビットずつ変換する方法もあるが、PSHUFB が使えて POPCNT が使えない CPU は少なく、利用場面は限られる。

Stockfish†によれば、 POPCNT がない場合は 16ビットずつに分けて表を引く方が (64KB の表とその初期化が必要になるが) 速いようだ。

Mirroring - 鏡像

Chess Programing Wiki - Flipping Mirroring and Rotating†
Arm には専用命令 (rbit) があるが、バイト内の鏡像にするために rev でバイトの反転を戻す必要がある。 (Neon の rbit はバイト内)

1バイトの鏡像

上記 Chess Programing Wiki にもあるが、 Bit Twiddling Hacks† にも Kindergarten + SWAR な方法が載っている。どちらのページでも 32 ビット用としては 4 ビットずつに分ける方法が紹介されているが、6 ビットと 2 ビットに分けた方が、2 ビットの方をシフトにできる。

	b = (((b * 0x200802) & 0x4422110) + ((b << 7) & 0x880)) * 0x01010101 >> 24;

PSHUFB(SSSE3) による鏡像

4ビットずつに分けた元データをシャッフルマスクにして、反転した4ビットを選ぶ。

	const __m128i mask0F0F = _mm_set1_epi16(0x0F0F);
	const __m128i mbitrev  = _mm_set_epi8(15, 7, 11, 3, 13, 5, 9, 1, 14, 6, 10, 2, 12, 4, 8, 0);
	bb = _mm_or_si128(_mm_shuffle_epi8(mbitrev, _mm_and_si128(_mm_srli_epi64(bb, 4), mask0F0F)),
		_mm_slli_epi64(_mm_shuffle_epi8(mbitrev, _mm_and_si128(bb, mask0F0F)), 4));

BSWAP による上下反転

BSWAP はエンディアン変換のための命令だが、ビットボードに適用すると x86-64 では 1 命令で盤の上下を反転できる。

#ifdef _MSC_VER
	#define	vertical_mirror(x)	_byteswap_uint64(x)
#else
	#define	vertical_mirror(x)	__builtin_bswap64(x)
#endif

AVX2 によるX-Y軸の入れ替え

A1-H8 (初期配置の白石の延長なのでホワイトラインと呼ばれる) を軸とする反転。上下・左右の反転と組み合わせると回転になる。
Chess Programing Wiki には Flip about the Anti-Diagonal† として delta swap 3 回の方法が載っているが、 AVX2 では PMOVMSKB で縦方向のビットを拾っていくことができる。

unsigned long long transpose(unsigned long long b)
{
	__m256i	v = _mm256_sllv_epi64(_mm256_broadcastq_epi64(_mm_cvtsi64_si128(b)),
		_mm256_set_epi64x(0, 1, 2, 3));
	return ((unsigned long long) _mm256_movemask_epi8(v) << 32)
		| (unsigned int) _mm256_movemask_epi8(_mm256_slli_epi64(v, 4));
}

Mobility - 着手可能位置

打てる位置のビット集合がまとめて得られ、着手可能数を評価するときや、ゲーム木の展開時に使う。

左横方向, CPU (キャリー伝播)

横一列 8 ビットの MSB 方向については、 O & (P << 1) を O に加算すると、キャリー伝播により P に挟まれる O の並びが切れた位置が求められ、そこが空きなら打てる位置になる。

	mO = O & 0x7e7e7e7e7e7e7e7eULL;
	flip1 = mO & (P << 1);
	flip1 = mO + flip1;
	flip1 &= ~(P|O);	// mask with empties

右横方向, SSE2 (飽和減算)

acepck 氏に提供いただいたアイデア。
横一列 8 ビット中に、右が空きに接している相手 O が１か所のみだった場合に限れば、そのビットを O に加え、キャリー (O の切れた位置) と P の AND を取ってから加えたビットを飽和減算すると返る石のビットが得られる（P があると O に戻り、なかった場合は飽和で 0 になる）。それを右シフトして空きと AND すると打てる位置のビットが得られる。
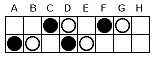mobility ..*O.*O.

打てる位置が生じるためには自分 - 相手 - 空きの並びが必要なので、8ビット中の打てる位置はたかだか 2ビットで、それぞれ C, D, E列、F, G, H列のいずれかに含まれる。なので SSE の 2レーンを使ってそれぞれの空きについて計算する。
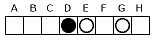mobility ...*O.O.

相手 - 空き - 相手 - 空きの並びがあると、 3ビット中に右が空きに接している相手 O が 2ビット生じる場合があり、減算する時に右の O も残ってしまうため、 PMINUB により左側のビットのみを残す。

	mOO = _mm_and_si128(OO, _mm_set1_epi64x(0x7e7e7e7e7e7e7e7eULL));
		// pick O whose right next is empty
	r1 = _mm_andnot_si128(_mm_slli_epi64(_mm_or_si128(PP, OO), 1), mOO);
		// split them into bit 1 - 3 and bit 4 - 6
	r1 = _mm_and_si128(r1, _mm_set_epi64x(0x7070707070707070ULL, 0x0e0e0e0e0e0e0e0eULL));
		// erase lower empty in case of E-O-E sequence
	r1 = _mm_min_epu8(r1, _mm_set_epi64x(0x4040404040404040ULL, 0x0808080808080808ULL));
		// get flip with carry propagation and saturate subtract
	flip = _mm_subs_epu8(_mm_and_si128(_mm_add_epi8(mOO, r1), PP), r1);
	MM = _mm_or_si128(MM, _mm_srli_epi64(flip, 1));

8 方向, SSE2 + CPU

MMX 時代の実装は Gunnar Andersson (Zebra の作者) によるソースコード例を参照。文中にもあるが、Richard Delorme (Edax の作者) が発案、Gunnar Andersson が改良したものに、私が Parallel Prefix を追加したもの。

x86-64 では 64 ビットになり CPU でも処理しやすくなったが、SSE2 が標準になったため心おきなく使える。
SSE2 では 64×2 で 2 方向ずつ処理できるが、別々のシフト数でシフトすることができないので、工夫が必要。
前述のとおり盤面の上下反転 vertical_mirror は x86-64 では BSWAP の一命令でできるが、ベクトルの一方を上下反転すると、9 ビット左シフトが 7 ビット右シフトになり、元の 7 ビット右シフトと並列処理できるようになる。
SSE 初期の CPU では SSE の実行が遅かったり、CPU と SSE で負荷を分散した方が有利な場合もあり、以下の例では SSE2 で斜め方向、CPU で縦・横方向を処理している。(SSE 8 方向、SSE 6 方向 + CPU 2 方向とする実装も可能。)
横に並べて書くとソースは横に長くなるが、人間の読みやすさを損なわずにコンパイラが並列最適化しやすいソースになる。

unsigned long long get_moves(const unsigned long long P, const unsigned long long O)
{
	unsigned long long moves, mO, flip1, pre1, flip8, pre8;
	__m128i	PP, mOO, MM, flip, pre;

	mO = O & 0x7e7e7e7e7e7e7e7eULL;
	PP  = _mm_set_epi64x(vertical_mirror(P), P);
	mOO = _mm_set_epi64x(vertical_mirror(mO), mO);
		/* shift=-9:+7 */								/* shift=+8 */			/* shift=+1 */
	flip = _mm_and_si128(mOO, _mm_slli_epi64(PP, 7));				flip8  = O & (P << 8);		flip1  = mO & (P << 1);
	flip = _mm_or_si128(flip, _mm_and_si128(mOO, _mm_slli_epi64(flip, 7)));		flip8 |= O & (flip8 << 8);	moves  = mO + flip1;
	pre  = _mm_and_si128(mOO, _mm_slli_epi64(mOO, 7));				pre8   = O & (O << 8);
	flip = _mm_or_si128(flip, _mm_and_si128(pre, _mm_slli_epi64(flip, 14)));	flip8 |= pre8 & (flip8 << 16);
	flip = _mm_or_si128(flip, _mm_and_si128(pre, _mm_slli_epi64(flip, 14)));	flip8 |= pre8 & (flip8 << 16);
	MM = _mm_slli_epi64(flip, 7);							moves |= flip8 << 8;
		/* shift=+9:-7 */								/* shift=-8 */			/* shift=-1 */
	flip = _mm_and_si128(mOO, _mm_srli_epi64(PP, 7));				flip8  = O & (P >> 8);		flip1  = mO & (P >> 1);
	flip = _mm_or_si128(flip, _mm_and_si128(mOO, _mm_srli_epi64(flip, 7)));		flip8 |= O & (flip8 >> 8);	flip1 |= mO & (flip1 >> 1);
	pre = _mm_srli_epi64(pre, 7);							pre8 >>= 8;			pre1   = mO & (mO >> 1);
	flip = _mm_or_si128(flip, _mm_and_si128(pre, _mm_srli_epi64(flip, 14)));	flip8 |= pre8 & (flip8 >> 16);	flip1 |= pre1 & (flip1 >> 2);
	flip = _mm_or_si128(flip, _mm_and_si128(pre, _mm_srli_epi64(flip, 14)));	flip8 |= pre8 & (flip8 >> 16);	flip1 |= pre1 & (flip1 >> 2);
	MM = _mm_or_si128(MM, _mm_srli_epi64(flip, 7));					moves |= flip8 >> 8;		moves |= flip1 >> 1;

	moves |= _mm_cvtsi128_si64(MM) | vertical_mirror(_mm_cvtsi128_si64(_mm_unpackhi_epi64(MM, MM)));
	return moves & ~(P|O);	// mask with empties
}

8 方向, AVX2

AVX2 では 4 方向同時に処理でき、また別々のシフト数が設定できるため、話が簡単。

unsigned long long get_moves(const unsigned long long P, const unsigned long long O)
{
	__m256i	PP, mOO, MM, flip_l, flip_r, pre_l, pre_r, shift2;
	__m128i	M;
	const __m256i shift1897 = _mm256_set_epi64x(7, 9, 8, 1);
	const __m256i mflipH = _mm256_set_epi64x(0x7e7e7e7e7e7e7e7e, 0x7e7e7e7e7e7e7e7e, -1, 0x7e7e7e7e7e7e7e7e);

	PP = _mm256_broadcastq_epi64(_mm_cvtsi64_si128(P));
	mOO = _mm256_and_si256(_mm256_broadcastq_epi64(_mm_cvtsi64_si128(O)), mflipH);

	flip_l = _mm256_and_si256(mOO, _mm256_sllv_epi64(PP, shift1897));
	flip_r = _mm256_and_si256(mOO, _mm256_srlv_epi64(PP, shift1897));
	flip_l = _mm256_or_si256(flip_l, _mm256_and_si256(mOO, _mm256_sllv_epi64(flip_l, shift1897)));
	flip_r = _mm256_or_si256(flip_r, _mm256_and_si256(mOO, _mm256_srlv_epi64(flip_r, shift1897)));
	pre_l = _mm256_and_si256(mOO, _mm256_sllv_epi64(mOO, shift1897));
	pre_r = _mm256_srlv_epi64(pre_l, shift1897);
	shift2 = _mm256_add_epi64(shift1897, shift1897);
	flip_l = _mm256_or_si256(flip_l, _mm256_and_si256(pre_l, _mm256_sllv_epi64(flip_l, shift2)));
	flip_r = _mm256_or_si256(flip_r, _mm256_and_si256(pre_r, _mm256_srlv_epi64(flip_r, shift2)));
	flip_l = _mm256_or_si256(flip_l, _mm256_and_si256(pre_l, _mm256_sllv_epi64(flip_l, shift2)));
	flip_r = _mm256_or_si256(flip_r, _mm256_and_si256(pre_r, _mm256_srlv_epi64(flip_r, shift2)));
	MM = _mm256_sllv_epi64(flip_l, shift1897);
	MM = _mm256_or_si256(MM, _mm256_srlv_epi64(flip_r, shift1897));

	M = _mm_or_si128(_mm256_castsi256_si128(MM), _mm256_extracti128_si256(MM, 1));
	M = _mm_or_si128(M, _mm_unpackhi_epi64(M, M));
	return _mm_cvtsi128_si64(M) & ~(P|O);	// mask with empties
}

8 方向, CPU

Arm64 では Neon も使えるが、シフト＋演算命令が強力なので 8 方向 CPU でやった方が速い。

unsigned long long get_moves(const unsigned long long P, const unsigned long long O)
{
	unsigned long long moves, mO;
	unsigned long long flip1, flip7, flip9, flip8, pre1, pre7, pre9, pre8;

	mO = O & 0x7e7e7e7e7e7e7e7eULL;
	flip7  = mO & (P << 7);		flip9  = mO & (P << 9);		flip8  = O & (P << 8);		flip1  = mO & (P << 1);
	flip7 |= mO & (flip7 << 7);	flip9 |= mO & (flip9 << 9);	flip8 |= O & (flip8 << 8);	moves  = mO + flip1;
	pre7 = mO & (mO << 7);		pre9 = mO & (mO << 9);		pre8 = O & (O << 8);
	flip7 |= pre7 & (flip7 << 14);	flip9 |= pre9 & (flip9 << 18);	flip8 |= pre8 & (flip8 << 16);
	flip7 |= pre7 & (flip7 << 14);	flip9 |= pre9 & (flip9 << 18);	flip8 |= pre8 & (flip8 << 16);
	moves |= flip7 << 7;		moves |= flip9 << 9;		moves |= flip8 << 8;
	flip7  = mO & (P >> 7);		flip9  = mO & (P >> 9);		flip8  = O & (P >> 8);		flip1  = mO & (P >> 1);
	flip7 |= mO & (flip7 >> 7);	flip9 |= mO & (flip9 >> 9);	flip8 |= O & (flip8 >> 8);	flip1 |= mO & (flip1 >> 1);
	pre7 >>= 7;			pre9 >>= 9;			pre8 >>= 8;			pre1 = mO & (mO >> 1);
	flip7 |= pre7 & (flip7 >> 14);	flip9 |= pre9 & (flip9 >> 18);	flip8 |= pre8 & (flip8 >> 16);	flip1 |= pre1 & (flip1 >> 2);
	flip7 |= pre7 & (flip7 >> 14);	flip9 |= pre9 & (flip9 >> 18);	flip8 |= pre8 & (flip8 >> 16);	flip1 |= pre1 & (flip1 >> 2);
	moves |= flip7 >> 7;		moves |= flip9 >> 9;		moves |= flip8 >> 8;		moves |= flip1 >> 1;

	return moves & ~(P|O);	// mask with empties
}

Get full lines - 埋まっている列を求める

一列全て埋まっていれば全ビット 1、そうでなければ全ビット 0。確定石の計算 (get_stability) で利用。

横方向, CPU

2 段の Parallel Prefix (Kogge-Stone)

	full &= full >> 1;
	full &= full >> 2;
	full &= full >> 4;
	return (full & 0x0101010101010101) * 0xff;

横方向, SSE2

MMX / SSE2 では一命令で可能。

	full = _mm_cmpeq_epi8(b, _mm_set1_epi8(0xff));

縦方向, CPU

ローテート + AND 3回

	full &= (full >> 8) | (full << 56);	// ror 8
	full &= (full >> 16) | (full << 48);	// ror 16
	full &= (full >> 32) | (full << 32);	// ror 32

(x >> n) | (x << (64 - n)) は n ビットローテート (n ≠ 0) のイディオムで、多くのコンパイラがローテート命令に落としてくれる。

結果の上位ワードと下位ワードは同じになるので、32 ビット CPU では、

	unsigned int	t = (unsigned int) full & (unsigned int)(full >> 32);
	t &= (t >> 16) | (t << 16);	// ror 16
	t &= (t >> 8) | (t << 24);	// ror 8
	full = t | ((unsigned long long) t << 32);

斜め方向, CPU

盤外は石があるものとし、左右から 2 段の Parallel Prefix で求める。±9 のみ 3 段目のマスクを共用できる。

	l7 = r7 = disc;
	l7 &= 0xff01010101010101 | (l7 >> 7);	r7 &= 0x80808080808080ff | (r7 << 7);
	l7 &= 0xffff030303030303 | (l7 >> 14);	r7 &= 0xc0c0c0c0c0c0ffff | (r7 << 14);
	l7 &= 0xffffffff0f0f0f0f | (l7 >> 28);	r7 &= 0xf0f0f0f0ffffffff | (r7 << 28);
	full_d7 = l7 & r7;

	l9 = r9 = disc;
	l9 &= 0xff80808080808080 | (l9 >> 9);	r9 &= 0x01010101010101ff | (r9 << 9);
	l9 &= 0xffffc0c0c0c0c0c0 | (l9 >> 18);	r9 &= 0x030303030303ffff | (r9 << 18);
	full_d9 = l9 & r9 & (0x0f0f0f0ff0f0f0f0 | (l9 >> 36) | (r9 << 36));

斜め方向, SSE2

Mobility のときと同様に、BSWAP で +7/-7 を -9/+9 に置き換える。 SSE には andnot があるので、ド・モルガンの定理で or - and を andnot - andnot に置き換え、マスクを反転すると 2 段目の左右で共用できるようになる。

	const __m128i e790 = _mm_set1_epi64x(0xff80808080808080);
	const __m128i e791 = _mm_set1_epi64x(0x01010101010101ff);
	const __m128i e792 = _mm_set1_epi64x(0x00003f3f3f3f3f3f);
	const __m128i e793 = _mm_set1_epi64x(0x0f0f0f0ff0f0f0f0);

	l79 = r79 = _mm_unpacklo_epi64(_mm_cvtsi64_si128(disc), _mm_cvtsi64_si128(vertical_mirror(disc)));
	l79 = _mm_and_si128(l79, _mm_or_si128(e790, _mm_srli_epi64(l79, 9)));
	r79 = _mm_and_si128(r79, _mm_or_si128(e791, _mm_slli_epi64(r79, 9)));
	l79 = _mm_andnot_si128(_mm_andnot_si128(_mm_srli_epi64(l79, 18), e792), l79);
	r79 = _mm_andnot_si128(_mm_slli_epi64(_mm_andnot_si128(r79, e792), 18), r79);
	l79 = _mm_and_si128(_mm_and_si128(l79, r79), _mm_or_si128(e793,
		_mm_or_si128(_mm_srli_epi64(l79, 36), _mm_slli_epi64(r79, 36))));
	full_d9 = _mm_cvtsi128_si64(l79);
	full_d7 = vertical_mirror(_mm_cvtsi128_si64(_mm_unpackhi_epi64(l79, l79)));

斜め方向, AVX2 (Kogge-Stone)

以下 static な __v4di を ULL で初期化するために共用体 V4DI を定義する。（unsigned long long のみだと 32 バイトアラインメントが保証されない。）

	typedef union {
		unsigned long long	ull[4];
		__m256i	v4;
	} V4DI;

±7と±9のシフトを一方向に揃える必要があるので、ここも PSHUFB で -7/-9 を +9/+7 に置き換える。

	const __m128i mcpyswap = _mm_set_epi8(0, 1, 2, 3, 4, 5, 6, 7, 7, 6, 5, 4, 3, 2, 1, 0);
	const __m128i mbswapll = _mm_set_epi8(8, 9, 10, 11, 12, 13, 14, 15, 0, 1, 2, 3, 4, 5, 6, 7);
	static const V4DI shiftlr[] = {{{ 9, 7, 7, 9 }}, {{ 18, 14, 14, 18 }}, {{ 36, 28, 28, 36 }}};
	static const V4DI e790 = {{ 0xff80808080808080, 0xff01010101010101, 0xff01010101010101, 0xff80808080808080 }};
	static const V4DI e791 = {{ 0xffffc0c0c0c0c0c0, 0xffff030303030303, 0xffff030303030303, 0xffffc0c0c0c0c0c0 }};
	static const V4DI e792 = {{ 0xfffffffff0f0f0f0, 0xffffffff0f0f0f0f, 0xffffffff0f0f0f0f, 0xfffffffff0f0f0f0 }};

	v4_disc = _mm256_castsi128_si256(_mm_shuffle_epi8(l81, mcpyswap));
	lr79 = _mm256_permute4x64_epi64(v4_disc, 0x50);	// disc, disc, rdisc, rdisc
	lr79 = _mm256_and_si256(lr79, _mm256_or_si256(e790.v4, _mm256_srlv_epi64(lr79, shiftlr[0].v4)));
	lr79 = _mm256_and_si256(lr79, _mm256_or_si256(e791.v4, _mm256_srlv_epi64(lr79, shiftlr[1].v4)));
	lr79 = _mm256_and_si256(lr79, _mm256_or_si256(e792.v4, _mm256_srlv_epi64(lr79, shiftlr[2].v4)));
	l79 = _mm_shuffle_epi8(_mm256_extracti128_si256(lr79, 1), mbswapll);
	l79 = _mm_and_si128(l79, _mm256_castsi256_si128(lr79));

斜め方向, AVX2 (PCMPEQQ)

横方向と同様に PCMPEQ を利用した例。わかりやすいが 4 ラインずつの処理なので Kogge-Stone に少し劣る。

	static const V4DI m791 = {{ 0x0402010000804020, 0x2040800000010204, 0x0804020180402010, 0x1020408001020408 }};	// V8SI
	static const V4DI m792 = {{ 0x0000008040201008, 0x0000000102040810, 0x1008040201000000, 0x0810204080000000 }};
	static const V4DI m793 = {{ 0x0000804020100804, 0x0000010204081020, 0x2010080402010000, 0x0408102040800000 }};
	static const V4DI m794 = {{ 0x0080402010080402, 0x0001020408102040, 0x4020100804020100, 0x0204081020408000 }};
	static const V2DI m795 = {{ 0x8040201008040201, 0x0102040810204080 }};

	v4_disc = _mm256_broadcastq_epi64(l81);
	lr79 = _mm256_and_si256(_mm256_cmpeq_epi32(_mm256_and_si256(v4_disc, m791.v4), m791.v4), m791.v4);
	lr79 = _mm256_or_si256(lr79, _mm256_and_si256(_mm256_cmpeq_epi64(_mm256_and_si256(v4_disc, m792.v4), m792.v4), m792.v4));
	lr79 = _mm256_or_si256(lr79, _mm256_and_si256(_mm256_cmpeq_epi64(_mm256_and_si256(v4_disc, m793.v4), m793.v4), m793.v4));
	lr79 = _mm256_or_si256(lr79, _mm256_and_si256(_mm256_cmpeq_epi64(_mm256_and_si256(v4_disc, m794.v4), m794.v4), m794.v4));
	l79 = _mm_and_si128(_mm_cmpeq_epi64(_mm_and_si128(_mm256_castsi256_si128(v4_disc), m795.v2), m795.v2), m795.v2);
	l79 = _mm_or_si128(l79, _mm_or_si128(_mm256_extracti128_si256(lr79, 1), _mm256_castsi256_si128(lr79)));

Count Last Flip - 最終手での返る石数

最終手（一か所空き）については返る石のビットを求める必要はなく、石数のみわかればよい。
探索深さの中の一手のみではあるが、探索木の末端で訪問数が多いため、最適化は効果がある。
最終手なので、実際に使われるのは隅近辺がほとんどになる。

Flip (Move Generator) の特殊例ではあるが、こちらの方が単純なので先に扱う。
最後の空きを除くと P でないビットは O なので、パラメータは一方でよい。一列分 8 ビットの P を集め、返る石数をテーブル (打つ位置により 8 種類) で引く。

Kindergarten bitboard†

乗算はシフト+加算なので、部分積が重ならないような乗数でビットの収集 (gather) が行える。発見的に求めた乗数 (magic number) でビットの収集を行う Magic bitboard に対し、Kindergarten bitboard と呼ばれる。

	// A8 TO A1, A8 TO H1
	n_flipped  = COUNT_FLIP[7][((P & 0x0101010101010101) * 0x0102040810204080) >> 56];
	n_flipped += COUNT_FLIP[0][((P & 0x0102040810204080) * 0x0101010101010101) >> 56];

32ビットCPU では64ビット乗算が複雑（ときにサブルーチンコール）になってしまうので、32ビット乗算に分解した方がよい。

	n_flipped  = COUNT_FLIP[7][(((LODWORD(P) & 0x01010101u) + ((HIDWORD(P) & 0x01010101u) << 4)) * 0x01020408u) >> 24];
	n_flipped += COUNT_FLIP[0][(((HIDWORD(P) & 0x01020408u) + (LODWORD(P) & 0x10204080u)) * 0x01010101u) >> 24];

90°/ 135° merge

たとえば D1 の場合、A3-D1 と D1-H4 の斜めをまとめて gather すると表を引く回数を1回減らせる。

	n_flipped  = COUNT_FLIP[3][((P & 0x0000008041221408ULL) * 0x0101010101010101ULL) >> 56];	// A3D1H4

A4 の場合、D1-A4-E8 は部分積のビットが干渉するので単純な kindergarten はできない。縦と組合わせて A1-A4-E8 と D1-A4-A8 にすると可能になる。

	n_flipped  = COUNT_FLIP[3][((P & 0x1008040201010101ULL) * 0x0102040808080808ULL) >> 56];	// A1A4E8
	n_flipped += COUNT_FLIP[4][((P & 0x0101010101020408ULL) * 0x1010101008040201ULL) >> 56];	// D1A4A8

LS1B isolation† の利用

マスごとに処理を分けるとき、片方向でいい場合には表引きを計算に変えられることもある。以下の LS1B と LZCNT はその例。

x & -x (= x & ~(x - 1)) が最下位ビット抽出のイディオムとして知られている。 BMI1 の CPU 命令にもあり、対応 CPU ではコンパイラにより一命令に最適化されることもある。
A1 から A8 方向に返る石数:

	// A1 to A8
	Pv = P & 0x0101010101010100ULL;
	n_flipped = ((Pv & -Pv) * 0x0000102030405060ULL) >> 60;

LZCNT, __builtin_clzll の利用

LZCNT は BMI にある、最上位から連続した 0 を数える命令。 P = 0 では 64 になるのでマスクで 0 にする。

	// A8 to A1
	n_flipped = __lzcnt64((P & 0x0080808080808080ULL) << 8) >> 3) & 0x07;

BSR や __builtin_clzll の場合は、0 を渡さないように番兵を使う。 P = 0 では 63 になるので 1 を加えてからマスクする。

	// A8 to A1
	n_flipped = ((__builtin_clzll((P & 0x0080808080808080ULL) | 1) + 1) >> 3) & 0x07;

BMI2 (PEXT)

AVX2 と同時期に導入された BMI2 にはビットを集めるための CPU 命令が追加され、kindergarten が要らなくなり、またマスごとに処理を分ける必要もなくなった。
ただし PEXT は Intel では高速だが、Zen2 までの AMD ではマイクロコード処理で非常に遅い†。

	P &= mask_x[pos][3];	// mask out unrelated bits to make dummy 0 bits for outside
	n_flipped  = COUNT_FLIP[x][(P >> (pos & 0x38)) & 0xFF];
	n_flipped += COUNT_FLIP[y][_pext_u64(P, mask_x[pos][0])];
	n_flipped += COUNT_FLIP[y][_pext_u64(P, mask_x[pos][1])];
	n_flipped += COUNT_FLIP[y][_pext_u64(P, mask_x[pos][2])];

SSE2 (PMOVMSKB, PSADBW) (_mm_movemask_epi8, _mm_sad_epu8)

PSADBW は動画圧縮などのための、 Byte * 8 の差の絶対値の合計を求める命令だが、一方を 0 として 8 バイトの水平加算に使える。
(このマスクの各バイトの最大値は 0x80 だが、0x80 の絶対値は 0x80 になりぎりぎりセーフ。)
PMOVMSKB は縦と斜めに、PSADBW は横と斜めに使えるので、4 方向中の斜めを振り分けると SSE2 への納まりがよい。
こちらも分岐なしで実装でき、ビットボードが SSE レジスターにある時は Intel の PEXT に近い性能が出る。

	I2 = _mm_sad_epu8(_mm_and_si128(PP, mask_hdvd[pos][0]), _mm_setzero_si128());
	n_flipped  = COUNT_FLIP[x][_mm_cvtsi128_si32(I2)];
	n_flipped += COUNT_FLIP[x][_mm_extract_epi16(I2, 4)];
	i = _mm_movemask_epi8(_mm_sub_epi8(_mm_setzero_si128(), _mm_and_si128(PP, mask_hdvd[pos][1])));
	n_flipped += COUNT_FLIP[y][i >> 8];
	n_flipped += COUNT_FLIP[y][i & 0xFF];

AVX512VL だと後半に _mm_movemask_epi8 に代えて _mm_test_epi8_mask (VPTESTMB) が使える。

    	i = _cvtmask16_u32(_mm_test_epi8_mask(PP, mask_hdvd[pos][1]));
	n_flipped += COUNT_FLIP[y][i >> 8];
	n_flipped += COUNT_FLIP[y][i & 0xFF];

AVX2 が使えるとき CPU で横方向、VPMOVMSKB で残り 3 方向を求めることもできるが、 CPU のステップはそれなりに必要 (ここは BEXTR や BZHI でも改善しない) で、また YMM を使うと VZEROUPPER† が入り、SSE2 とどちらがいいかは微妙。

	n_fliped = COUNT_FLIP[x][(P >> (pos & 0x38)) & 0xFF];
	i = _mm256_movemask_epi8(_mm256_sub_epi8(_mm256_setzero_si256(), _mm256_and_si256(PP, mask_hdvd[pos])));
	n_flipped += COUNT_FLIP[y][i >> 24];
	n_flipped += COUNT_FLIP[y][(i >> 16) & 0xFF];
	n_flipped += COUNT_FLIP[y][i & 0xFF];

Arm Neon (vaddvq)

Arm Neon には PMOVMSKB にあたる命令はないが、ベクトルの水平総和 vaddvq はある (aarch64 のみ。aarch32 では水平加算 3 回で代用) ので、4 方向ともそれを使う。 vaddvq_u8 では 16 バイトの総和になってしまうので、vzipq_u8 でインターリーブしてから vaddvq_u16 を用い、 16 ビット内の上位バイトと下位バイトで並列演算（分割統治）を行う。（マスクもインターリーブしておく。）

#ifndef __aarch64__
#define vaddvq_u16(x)	vget_lane_u64(vpaddl_u32(vpaddl_u16(vadd_u16(vget_high_u16(x), vget_low_u16(x)))), 0)
#endif

	const uint8x16_t dmask = { 1, 1, 2, 2, 4, 4, 8, 8, 16, 16, 32, 32, 64, 64, 128, 128 };

	PP = vzipq_u8(PP, PP).val[0];
	II = vreinterpretq_u16_u64(vandq_u64(vreinterpretq_u64_u8(PP), mask_dvhd[pos][0]));
	t0 = vaddvq_u16(II);
	n_flips  = COUNT_FLIP[x][t0 >> 8];
	n_flips += COUNT_FLIP[x][t0 & 0xFF];
	II = vreinterpretq_u16_u8(vandq_u8(vtstq_u8(PP, vreinterpretq_u8_u64(mask_dvhd[pos][1])), dmask));
	t1 = vaddvq_u16(II);
	n_flips += COUNT_FLIP[y][t1 >> 8];
	n_flips += COUNT_FLIP[y][t1 & 0xFF];

手番側が打てないときは相手側で同じ処理を行うことになるが、このときビットの収集を省略し、集めたビットを反転して求めることもできる。（斜めは盤内のみ。また最後の空きはテーブルで Don't care になるようにしておく。）
x86-64 ではメリットは少ないが、ビット収集のコストが高く、スクラッチレジスターの多い Arm64 では使える。

	m = o_mask[pos];	// valid diagonal bits
	n_flips  = COUNT_FLIP[x][(t0 >> 8) ^ 0xFF];
	n_flips += COUNT_FLIP[x][(t0 ^ m) & 0xFF];
	n_flips += COUNT_FLIP[y][(t1 ^ m) >> 8];
	n_flips += COUNT_FLIP[y][(~t1) & 0xFF];

AVX512CD/VL (VPLZCNTQ)

AVX512CD/VL による Flip がコンパクトになったため、AVX512CD/VL が使える環境では最終手も Flip の POPCNT で求めるのも有力になった。
最終手なので途中の空きを考慮する必要はなく、挟めるかどうかは線上に P があるかどうかで判断できる。

int last_flip(int pos, unsigned long long P)
{
	__m256i PP = _mm256_set1_epi64x(P);
	__m256i	flip, outflank, eraser, rmask, lmask;
	__m128i	flip2;

		// left: look for player LS1B
	lmask = lmask_v4[pos];
	outflank = _mm256_and_si256(PP, lmask);
		// set below LS1B if P is in lmask
	flip = _mm256_maskz_add_epi64(_mm256_test_epi64_mask(PP, lmask), outflank, _mm256_set1_epi64x(-1));
	// flip = _mm256_and_si256(_mm256_andnot_si256(outflank, flip), lmask);
	flip = _mm256_ternarylogic_epi64(outflank, flip, lmask, 0x08);

		// right: look for player bit with lzcnt
	rmask = rmask_v4[pos];
	eraser = _mm256_srlv_epi64(_mm256_set1_epi64x(-1),
		_mm256_maskz_lzcnt_epi64(_mm256_test_epi64_mask(PP, rmask), _mm256_and_si256(PP, rmask)));
	// flip = _mm256_or_si256(flip, _mm256_andnot_si256(eraser, rmask));
	flip = _mm256_ternarylogic_epi64(flip, eraser, rmask, 0xf2);

	flip2 = _mm_or_si128(_mm256_castsi256_si128(flip), _mm256_extracti128_si256(flip, 1));
	return 2 * bit_count(_mm_cvtsi128_si64(_mm_or_si128(flip2, _mm_unpackhi_epi64(flip2, flip2))));
}

手番側と相手側（手番側がパスだった時に使う）を並行して求めることもでき、将来 512bit 処理が速い CPU があれば連結した 512bit で処理することもできる。
両者パスのとき、空きを石数の多い方に加える処理は、石数が 32～63 のときに 1、すなわちビット 5 を加えればよい。

int board_score_1(unsigned long long P, int pos)
{
	int	score;
	__m512i	op_outflank, op_flip, op_eraser, mask;
	__m256i	o_flip, opop_flip;
	__m128i	OP;
	__mmask8 op_pass;
	__m512i	O4P4 = _mm512_xor_si512(_mm512_set1_epi64(P), _mm512_set_epi64(-1, -1, -1, -1, 0, 0, 0, 0));

		// left: look for player LS1B
	mask = _mm512_broadcast_i64x4(lrmask[pos].v4[0]);
	op_outflank = _mm512_and_si512(O4P4, mask);
		// set below LS1B if P is in lmask
	op_flip = _mm512_maskz_add_epi64(_mm512_test_epi64_mask(op_outflank, op_outflank),
		op_outflank, _mm512_set1_epi64(-1));
	// op_flip = _mm512_and_si512(_mm512_andnot_si512(op_outflank, op_flip), mask);
	op_flip = _mm512_ternarylogic_epi64(op_outflank, op_flip, mask, 0x08);

		// right: clear all bits lower than outflank
	mask = _mm512_broadcast_i64x4(lrmask[pos].v4[1]);
	op_outflank = _mm512_and_si512(O4P4, mask);
	op_eraser = _mm512_srlv_epi64(_mm512_set1_epi64(-1),
		_mm512_maskz_lzcnt_epi64(_mm512_test_epi64_mask(op_outflank, op_outflank), op_outflank));
	// op_flip = _mm512_or_si512(op_flip, _mm512_andnot_si512(op_eraser, mask));
	op_flip = _mm512_ternarylogic_epi64(op_flip, op_eraser, mask, 0xf2);

	o_flip = _mm512_extracti64x4_epi64(op_flip, 1);
	opop_flip = _mm256_or_si256(_mm256_unpacklo_epi64(_mm512_castsi512_si256(op_flip), o_flip),
		_mm256_unpackhi_epi64(_mm512_castsi512_si256(op_flip), o_flip));
	OP = _mm_xor_si128(_mm512_castsi512_si128(O4P4),
		_mm_or_si128(_mm256_castsi256_si128(opop_flip), _mm256_extracti128_si256(opop_flip, 1)));
	op_pass = _mm_cmpeq_epi64_mask(OP, _mm512_castsi512_si128(O4P4));
	OP = _mm_mask_unpackhi_epi64(OP, op_pass, OP, OP);	// use O if p_pass
	score = bit_count(_mm_cvtsi128_si64(OP));
		// last square for P if not P pass or (O pass and score >= 32)
	// score += ((~op_pass & 1) | ((op_pass >> 1) & (score >= 32)));
	score += (~op_pass | ((op_pass >> 1) & (score >> 5))) & 1;
	return score * 2 - SCORE_MAX;	// = bit_count(P) - (SCORE_MAX - bit_count(P))
}

Flip - 返る石を求める (Move Generator)

終盤探索 Endgame で費やす時間が多く、最適化の効果が大きい部分。クロック単位の差が速度に現れる。
基本的なアルゴリズムとしては、打つ位置の隣のマスから相手の石が続く間その隣を見ていき、切れた位置に自石があれば間が返す石になる。
条件分岐を並べて書く†のは容易だが、分岐数が多くかつ予測が効きにくい形なので、できるだけ分岐なしで書きたい。

Outflank - Flip テーブル参照による方法

多くのトッププログラムで採用されている方法。テーブル参照は複数回必要だが、左右方向同時に求められるので、以下の各方法と比べても大きく劣ることはない。
以下 Edax のコメントの訳。Outflank は敵を包囲する（部隊）の意。

盤の各マスに関数が用意される。高速なアクセスのため関数は配列化される。関数の一般形はプレイヤーと相手のビットボードを入力とし、返る石のビットボードを返す。
以下の記法を用いる:

x = 打つ位置

P = 自分の石のビットパターン

O = 相手の石のビットパターン

基本的な原理は着手の結果を配列として持っておく。連続した一列ではこれは容易で、このような配列にする:
 ARRAY[x][8-bits disc pattern];
残る問題は 64 ビットのディスクパターンの任意のラインを 8 ビットパターンに変換する方法になる。これを行う高速な方法は、所望のラインをビットマスクにより選び、得られたビットを単純な乗算と右シフトにより連続したビットに集め、0 から 255 の数値に直す方法である。 8 ビットディスクパターンが得られたら、第一の配列 (OUTFLANK) を用いて、相手の石を囲む自分の石を求める。
 outflank = OUTFLANK[x][O] & P;
この結果が自分の石に挟まれて返る石を与える第二の配列のインデックスになる。
 flipped = FLIPPED[x][outflank];
最後に、あらかじめ計算した変換配列により 8 ビットのビットパターンを 64 ビットディスクパターンに戻し、それぞれのラインで返る石を集めて結果を返す。

「64ビットのディスクパターンの任意のラインを8ビットパターンに変換する方法」は、前述の Kindergaten 、BMI2 の PEXT、 SSE2 (PMOVMSKB, PSADBW)を使う方法などがある。

Flip の outflank - flipped のテーブルは、outflank は打つ位置とその隣には発生しないので、 outflank をローテートして持つとサイズを節約できる。 kindergarten ではビットパターンが繰り返し現れるので、ローテートを同時に行えることもある。（乗算を使うためビットを右に動かすことはできないので、MSB 付近のビットの行き先によっては不可。）

	outflank_d &= ((P & 0x2050880402010000) * 0x0101010101010101) >> 55;	// (A3F8H6) hgfe[dcbah]g0edcba...

シフトの繰り返しによる方法

以下は一方向ずつ処理する方法。
Mobility と同様に、シフトの繰り返しで挟まれる石を集める例。 0x7e によるマスク（左右端での折り返しを防ぐ）は垂直方向(±8)には入れない。
左右両方向に使えるし、テーブルを必要としない方法。

	mO = O & 0x7e7e7e7e7e7e7e7e;	// except for vertical
	flip = (X << 1) & mO;		// 0 0 0 0 0 0 G 0
	flip |= (flip << 1) & mO;	// 0 0 0 0 0 F&G G 0
	flip |= (flip << 1) & mO;	// 0 0 0 0 E&F&G F&G G 0
	flip |= (flip << 1) & mO;
	flip |= (flip << 1) & mO;
	flip |= (flip << 1) & mO;
	flip |= (flip << 1) & mO;	// 0 B&C&D&E&F&G .. F&G G 0
	outflank = P & (flip << 1);
	if (outflank == 0)
		flip = 0;

Parallel Prefix

相手の石の隣同士の AND を取っておくと、少し高速化できる。
最後の if は（コンパイラが分岐を除くこともあるが）明示的に論理演算に代えておく。

	mO = O & 0x7e7e7e7e7e7e7e7e;
	flip = (X << 1) & mO;		// 0 0 0 0 0 0 G 0
	flip |= (flip << 1) & mO;	// 0 0 0 0 0 F&G G 0
	pre = mO & (mO << 1);		// A&B B&C C&D D&E E&F F&G G&H 0
	flip |= (flip << 2) & pre;	// 0 0 0 D&E&F&G E&F&G F&G G 0
	flip |= (flip << 2) & pre;	// 0 B&C&D&E&F&G .. F&G G 0
	outflank = P & (flip << 1);
	flip &= - (int) (outflank != 0);

キャリー伝播 (MSB 方向のみ)

Parallel Prefix は加算器の高速化に使われる技法だが、「あるビットから下がすべて 1 の場合のみ 1」は、全加算器の lookahead carry と同じ。 MSB 方向について、加算のキャリー伝播によりはさむ反対側の位置 Outflank を求められる。
求めたいビット以外を 1 で OR マスクすれば、7, 8, 9 方向も可能。SSE2 で 2 方向同時に処理できる。
SSE2 のキャリー伝搬ではマスクは反転して持った方がよい。andnot はあるが ornot はないため。

	mO = O | ~M;			// x0111
	outflank = (mO + 1) & M;	// 01000
	outflank &= P;			// 0P000
	flip = (outflank - (int) (outflank != 0)) & M;	// Outflank to Flip

LS1Bの利用 (MSB 方向のみ)

相手の石の反転にマスクをかけて LS1B を取り出すと、相手の石が切れた位置 Outflank がわかるので、自分の石と and を取ると、キャリー伝搬と同様の結果が得られる。

	outflank = ~O & M;
	outflank &= -outflank;		// LS1B
	outflank &= P;
	flip = (outflank - (int) (outflank != 0)) & M;	// Outflank to Flip

数学的に変形しても、この 2 方式が等価であることがわかる。

	((~O & M) & -(~O & M)) & P		// LS1B
	((~O & M) & (~(~O & M) + 1)) & P	// -x = (~x + 1)
	(~O & M & ((O | ~M) + 1)) & P		// De Morgan
	(((O | ~M) + 1) & M) & (P & ~O)		// P & O = 0, so P & ~O = P
	(((O | ~M) + 1) & M) & P		// carry propagation

キャリー伝搬と LS1B の演算量はほぼ同じだが、コンパイル結果はレジスターの使い方の違いなどで一方がよくなることがあるので、落ちたコードを見ながら使い分ける。

LZCNT (LSB 方向のみ)

Count Last Flip でも扱ったが、LZCNT は BMI にある、最上位から連続した 0 を数える命令。

	(0x8000000000000000ULL >> _lzcnt_u64(~O & (maskr)))

で相手の石が切れる位置を求めることができる。
厳密には LZCNT の引数が 0 のとき、シフト数が 64 となり、C 言語的には結果は未定義になる。ただし実際の CPU の実装では 64 ビットシフトして 0 になるか、modulo 64 でシフトしないかのどちらかで、マスクがあるのでどちらの場合でも処理上は問題ない。

__builtin_clzll (LSB 方向のみ)

gcc のビルトイン関数 __builtin_clzll や、x86 標準の CPU 命令 BSR (_BitScanReverse) は、LZCNT と同様の機能だが、引数が 0 のとき未定義になる。（BSR ではゼロフラグで返される）。__builtin_clzll(x) の周辺で、x ≠ 0 を利用した最適化が行われることもある。
前述のコードで、O の最後（辺）のビットをクリアしておけば引数が 0 になるのを防げる。 O が辺まで続いていた場合は辺に偽の outflank が生じるが、このとき辺に P はないので、P との AND を取るときに 0 になる。

	(0x8000000000000000ULL >> __builtin_clzll(((O) & (((maskr) & ((maskr) - 1)))) ^ (maskr)))

((maskr) & ((maskr) - 1)) は最下位ビットクリア (BLSR) のイディオム。maskr が定数なので定数になる。
その後 maskr を xor して、最下位ビットを立て、同時にその他のビットを反転している。

浮動小数変換 (MS1B) (LSB 方向のみ)

LZCNT は CPU を限定するし、SIMD にもできない（AVX512CD で追加された）。また BSWAP + LS1B も PSHUFB が SSSE3 以上なので、SSE2 では別の方法を使う。
SSE では浮動小数も使えるが（むしろそちらが本来の用途）、整数を浮動小数に変換して、指数部から BSR† を求めることができる。また、仮数部をクリアして整数に戻すと最上位の 1 ビットのみが残る。（最上位の 1 ビットがケチ表現†で隠れていたため。）
ただし 1 が仮数部に納まらないほど連続すると、丸めにより誤差が出ることがある（スマートな回避法はこちら†。これを繰り返すと PP fill）。この用途ではマスクをかけた値を渡すのでその心配はない。
SSE2 には符号付き 32 ビットしかないので、31 ビット長まで可能。3 命令でスループットも良好だが、レイテンシーはやや大きい。

static inline __m128i MS1B_epu31(const __m128i x) {
	const __m128 exp_mask = _mm_castsi128_ps(_mm_set1_epi32(0xff800000));
	return _mm_cvtps_epi32(_mm_and_ps(_mm_cvtepi32_ps(x), exp_mask));	// clear mantissa = non msb bits
}

32ビット入力にするには、負の時に符号ビットだけを返すようにする。7 命令。

static inline __m128i MS1B_epu32(const __m128i x) {
	__m128i y = MS1B_epu31(x);
	return _mm_andnot_si128(_mm_srli_epi32(_mm_srai_epi32(y, 31), 1), y);	// clear except sign if negative
}

C4, D4, E4, F4, C5, D5, E5, F5 の 8 マスは 8 方向すべてを調べなければいけないマスだが、それぞれの方向が 32 ビットに納まるので、MSB 方向はキャリー伝搬、LSB 方向は浮動小数変換で 4 並列ずつ効率よく行える。ただしこれらのマスは最初から石がある（呼ばれないコードで、テストプログラムでないとテストもできない）か、序盤で埋まるので速度への寄与はほぼない。

64ビットベクターからの変換は、AVX512 にしかない。64 ビットスカラーからの変換は x86-64 の SSE2 にはあるが、SIMD でなく CPU レジスターからしかできない。上記の 32 ビットを組み合わせれば可能だが、12 命令とやや長くなる。

static inline __m128i MS1B_epu64(const __m128i x) {
	__m128i y = MS1B_epu32(x);
	return _mm_and_si128(y, _mm_cmpeq_epi32(_mm_srli_epi64(y, 32), _mm_setzero_si128()));	// clear low if high != 0
}

52 ビットまでなら、ビット操作により強引に浮動小数に変換する方法で、7 命令でできる。
Intel Develper Zone - Int64 double conversion with SSE?†
StackOverflow - How to efficiently perform double/int64 conversions with SSE/AVX?†

static inline __m128i MS1B_epu52(const __m128i x) {
	const __m128d k1e52 = _mm_set1_pd(0x0010000000000000);
	const __m128d exp_mask = _mm_castsi128_pd(_mm_set1_epi64x(0xfff0000000000000));
	__m128d f;
	f = _mm_or_pd(_mm_castsi128_pd(x), k1e52);	// construct double x + 2^52
	f = _mm_sub_pd(f, k1e52);	// extract 2^52 from double -- mantissa will be automatically normalized
	f = _mm_and_pd(f, exp_mask);	// clear mantissa = non msb bits
	f = _mm_add_pd(f, k1e52);	// add 2^52 to push back the msb
	f = _mm_xor_pd(f, k1e52);	// remove exponent
	return _mm_castpd_si128(f);
}

Outflank → Flip (MSB方向)

反対側の自分の石の 1 ビットが求まったら、そこから上・下方向の全ビットをセットし、求める方向のビットマスクと AND を取ればよい。
Outflank より上のビットをセットするには、-2 を掛ければよい。

	// H8 to H1 (with LZCNT)
	outflank_v = (0x8000000000000000ULL >> _lzcnt_u64(~O & (0x0080808080808080))) & P;
	flipped  = (outflank_v * -2) & 0x0080808080808080;

SSE2 では64ビット乗算がないので、2 倍して 0 から引く（または 2 倍して 1 を引いて andnot する）。 32 ビット乗算も SSE2 では 2 レーンまで（4 レーン乗算は SSE4 以降）なので、4 並列の場合は同様。

	// (A8 to H1, A8 to A1) 
	const __m128i mask = _mm_set_epi64x(0x0002040810204080, 0x0001010101010101);
	outflank_vd = _mm_and_si128(MS1B_epu52(_mm_andnot_si128(OO, mask)), PP);
	flipped = _mm_and_si128(_mm_sub_epi64(_mm_setzero_si128(), _mm_add_epi64(outflank_vd, outflank_vd)), mask);

被減数の途中のビットを立てるとパーティショニングでき、3 方向以上同時に処理できることもある。

	// (G7 to A1, G7 to G1, G7 to A7)
	outflank = MS1B_epu52(_mm_andnot_si128(OO, _mm_set_epi64x(0x0000404040404040, 0x0000201008040201)));
	outflank = _mm_or_si128(outflank, MS1B_epu31(_mm_andnot_si128(OO, _mm_set_epi32(0, 0, 0x003f0000, 0))));
	outflank = _mm_and_si128(outflank, PP);

	flipped = _mm_sub_epi64(_mm_set_epi64x(0, 0x0000800000000000), _mm_add_epi64(outflank, outflank));
	flipped = _mm_and_si128(flipped, _mm_set_epi64x(0x0000404040404040, 0x003e201008040201));

Outflank → Flip (LSB方向)

Outflank より下のビットをセットするには、Outflank != 0 のときのみ 1 を引く。

	// A1 to A8
	outflank_v = ((O | ~0x0101010101010100ULL) + 1) & P & 0x0101010101010100;
	flipped = (outflank_v - (unsigned int) (outflank_v != 0)) & 0x0101010101010100;

定数 x に対する (unsigned long long) ~x は、x が 32 ビットに納まる場合には int でビット反転してから unsigned long long に拡張されるので、この例はそうではないが、64ビット演算を明示するために ULL が必要な場合がある。
SSE2 により2方向同時に処理できるが、PCMPEQQ は SSE4.1 以上なので SSE2 (x86-64) 汎用には使えない。 Outflank は 1 があるのは上下 DWord のどちらかのみなので、スワップして PCMPEQD する。

/**
 * Make inverted flip mask if opponent's disc are surrounded by player's.
 *
 * 0xffffffffffffffffULL (-1) if outflank is 0
 * 0x0000000000000000ULL ( 0) if a 1 is in 64 bit
 */
static inline __m128i flipmask (const __m128i outflank) {
	return _mm_cmpeq_epi32(_mm_shuffle_epi32(outflank, 0xb1), outflank);
}

「Outflank != 0 のときのみ 1 を引く」はうまくいくと 3 ～ 4 命令に最適化されるが、分岐のあるコードになるなどコンパイル結果が思わしくない場合には、代わりに構わず 1 を引き、Outflank = 0 の場合のみ MSB が 1 になるので、 MSB を LSB までシフトして足し戻す方法もある。
アセンブラ (CPU) またはキャリー付き演算の intrinsic が使える場合は 1 を引いてからキャリーを加えればよい。 intrinsic だと長く見えるが、正しく最適化されれば 2 命令。

#if __has_builtin(__builtin_subcll)
static inline unsigned long long OutflankToFlipmask(unsigned long long outflank) {
	unsigned long long flipmask, cy;
	flipmask = __builtin_subcll(outflank, 1, 0, &cy);
	return __builtin_addcll(flipmask, 0, cy, &cy);
}
#elif (defined(_M_X64) && (_MSC_VER >= 1800)) || (defined(__x86_64__) && defined(__GNUC__) && (__GNUC__ > 7 || (__GNUC__ == 7 && __GNUC_MINOR__ >= 2)))
static inline unsigned long long OutflankToFlipmask(unsigned long long outflank) {
	unsigned long long flipmask;
	unsigned char cy = _subborrow_u64(0, outflank, 1, &flipmask);
	_addcarry_u64(cy, flipmask, 0, &flipmask);
	return flipmask;
}
#else
	#define OutflankToFlipmask(outflank)	((outflank) - (unsigned int) ((outflank) != 0))
#endif

欲しいビット長が限られている場合、たとえば 8 ビットの場合は、0xff を掛けて 8 ビット右シフトすればよい（上位側に8ビットの余裕が必要）。 8 ビット右シフトしたものを減算するのも等価（下位側に 8 ビットの余裕が必要）。
SSE2 の PMULHUW を使えば 0xffff の乗算と16ビット右シフトが同時に行える。

飽和減算 (PSUBUSB) (_mm_subs_epu8)

今のところ AVX2 が利用できない場合は、訪問数の多い隅周辺で処理が軽くなることもあり、マスごとに 64 通りに場合分けした方が速いようだ。ジャンプテーブルを使う方法は、CPU の種類による実行時のディスパッチにも好都合。
ここからは特定のマスに適用できる SSE2 の小ネタをいくつか挙げる。

LSB 方向の Outflank → Flip で飽和減算を利用すると、0 から減算しても 0 なので、「Outflank != 0 のときのみ」の条件が省略できる。
飽和減算は Word までしかないので、利用できるのは横方向のみだが、キャリー伝搬と合わせて 4 命令で Flip 1 方向が求められる。

	// A1 to H1
	const __m128i next_h = _mm_set_epi64x(0, 0x0000000000000002);	// B1
	outflank_h = _mm_and_si128(_mm_add_epi8(O, next_h), P);
	flipped = _mm_subs_epu8(outflank_h, next_h);

PMULLW (_mm_mullo_epi16)

たとえば C1-A3 のように挟まれる石が１つの場合、P をシフトして O との and を取ればよいが、複数方向にある場合はそれぞれ別のシフト数が必要になる。
AVX2 にある Variable shift は SSE2 にはないが、乗算の乗数でばらばらの左シフトが行えることがある。空いたレーンでは Outflank → Flip などが同時に行える。

	// C1-B1-A1, C1-B2-A3, C1 to H1
	outflank_h = _mm_and_si128(_mm_add_epi8(OO, _mm_set_epi64x(0, 0x0000000000000008), PP);
	flipped_h_b1b2 = _mm_unpacklo_epi64(outflank_h, PP);
	flipped_h_b1b2 = _mm_srli_epi64(_mm_mullo_epi16(flipped_h_b1b2, _mm_set_epi16(0, 0, 0x0002, 0x0200, 0, 0, 0, 0x00ff)), 8);
	flipped_h_b1b2 = _mm_and_si128(_mm_and_si128(flipped_h_b1b2, OO), _mm_set_epi16(0, 0, 0, 0x0202, 0, 0, 0, 0x0078));

前出 MS1B_epu52 で相手の石の切れ目を探せるのは 52 ビット以下だが、唯一対角線の G7-A1 が 55 ビットある。これは乗算による可変シフトで圧縮・伸長でき、MS1B_epu64 を使うより短くなる。

	// H8 to H1, H8 to A1
	outflank = _mm_andnot_si128(OO, _mm_set_epi64x(0x0080808080808080, 0x0040201008040201));
	outflank = _mm_srli_epi16(_mm_mullo_epi16(outflank, _mm_set_epi16(1, 1, 1, 1, 1, 1, 16, 16)), 4);
	outflank = _mm_mullo_epi16(MS1B_epu52(outflank), _mm_set_epi16(16, 16, 1, 1, 16, 16, 16, 16));

PMULHUW (_mm_mulhi_epu16), PMINSW (_mm_min_epi16)

PMULLW は左シフトの代用だが、右シフトを代用したいときには PMULHUW (_mm_mulhi_epu16) が利用できる。

	// D6-C7-B8, D6-E7-F8
	flipped_c7e7 = _mm_and_si128(_mm_mulhi_epu16(PP, _mm_set_epi16(0x0080, 0, 0, 0, 0x0200, 0, 0, 0)), OO);
	flipped_c7e7 = _mm_and_si128(flipped_c7e7, _mm_set_epi64x(0x0010000000000000, 0x0004000000000000));

だがこの例では PMINSW (_mm_min_epi16) を利用する方がシンプル。P と O の両方があるとき (小さい方の) O になり、それ以外ではゼロになる。

	// D6-C7-B8, D6-E7-F8
	flipped_c7e7 = _mm_min_epi16(_mm_and_si128(PP, _mm_set_epi64x(0x0200000000000000, 0x2000000000000000)),
		_mm_and_si128(OO, _mm_set_epi64x(0x0004000000000000, 0x0010000000000000)));

PMINUB (_mm_min_epu8)

PMULHUW による可変右シフトでは各レーン 1 以上右シフトしなければならず、シフトしないレーンを作れない。このため前記 H8 to A1 の例では PMULLW と PSRLQ の 2 命令になってしまったが、PMINUB を使えば 1 命令で済む。

	// H8 to H1, H8 to A1
	outflank = _mm_andnot_si128(OO, _mm_set_epi64x(0x0080808080808080, 0x0040201008040201));
	outflank = _mm_min_epu8(outflank, _mm_set_epi64x(0x0008080808080808, 0x0004020108040201));
	outflank = _mm_mullo_epi16(MS1B_epu52(outflank), _mm_set_epi16(16, 16, 16, 16, 16, 16, 1, 1));

積和演算 (PMADDWD) (_mm_madd_epi16)

C3, F3, C6, F6 の 4 マスは 5 方向に一石返しがあり、積和演算が使える。（だが序中盤で埋まるマスで、性能への寄与はほとんどない。）

	// from C3
	flipped_b4b3b2c2d2 = _mm_and_si128(_mm_shufflelo_epi16(PP, 0x90), _mm_set_epi16(0, 0, 0, 0x0001, 0x0001, 0x0001, 0x0004, 0x0010));	// ...a1a5a3c1e1
	flipped_b4b3b2c2d2 = _mm_madd_epi16(flipped_b4b3b2c2d2, _mm_set_epi16(0, 0, 0, 0x0200, 0x0200, 0x0002, 0x0100, 0x0080));
	flipped_b4b3b2c2d2 = _mm_and_si128(_mm_shufflelo_epi16(flipped_b4b3b2c2d2, 0xf8), OO);

飽和加算 (PADDUSB) (_mm_adds_epu8)

例えば B3 から、キャリー伝搬のために bit 18 を加算すると同時に、B2 と C2 の flip を取るために rank 1 にマスクを掛けたい。 or と add の 2 命令で可能だが、飽和加算を使うと 1 命令でできる。

	// B3-B2-B1, B3-C2-D1, B3 to H3
	outflank_h = _mm_and_si128(PP, _mm_adds_epu8(OO, _mm_set_epi8(0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 4, 0, -1)));
	flipped_h_b2c2 = _mm_srli_epi16(_mm_mullo_epi16(outflank_h, _mm_set_epi16(0, 0, 0, 0x1000, 0, 0, 0x001f, 0x2000)), 5);
	flipped_h_b2c2 = _mm_and_si128(flipped_h_b2c2, _mm_set_epi64x(0x0000000000000400, 0x00000000007c0200));

ただし O の C3～H3 が埋まっているときの考慮が必要。レーン 3 も飽和し、A3 に偽の outflank が生じるが、flip はシフトアウトされる。

PACKUSWB (_mm_packus_epi16)

F8-G7-H6 と F8-G8-H8 のように、16 ビット離れた自石で 8 ビット離れた相手の石を返したいことがある。
乗算によるシフトや PMADDWD も使えるが、パック命令を使う方法もある。

	// F8-G7-H6, F8-G8-H8
	flipped_g7g8 = _mm_srli_epi64(_mm_and_si128(PP, _mm_set_epi64x(0x8000800000000000, 0)), 9);
	flipped_g7g8 = _mm_and_si128(_mm_packus_epi16(flipped_g7g8, _mm_setzero_si128()), OO);

SSE2 でのテーブル参照

これらの SSE2 最適化を行った上でも、マスによっては Outflank - Flip テーブル参照が最適な場合がある。
AVX2 にはテーブル参照のために VPGATHERQD があるが、SSE2 では使えないので、インデックスは PMOVMSKB, PSADBW により CPU レジスターに用意し、Outflank まではスカラー処理する。
Flip はまとめてマスクを掛けるために SSE レジスターの上位・下位それぞれにロードしたいが、 SSE2 の整数命令には上位 64 ビットのロードがない。（PUNPCKLQDQ xmm, m128 は 128-bit alignment を要求する。PINSRQ は SSE4.1 以上。）
Agner† によれば、ほとんどの CPU でメモリーからのロードの際には整数・小数混用のペナルティはないようなので、 MOVQ と MOVHPS を使うことにするが、ソース上は多くのキャストが必要になる。

static inline __m128i load64x2 (const unsigned long long *x0, const unsigned long long *x1) {
	return _mm_castps_si128(_mm_loadh_pi(_mm_castsi128_ps(_mm_loadl_epi64((__m128i *) x0)), (__m64 *) x1));
}

PSHUFD (_mm_shuffle_epi32)

64ビットの下位レーンから上位レーンへの複製は、PUNPCKLQDQ (_mm_unpacklo_epi64) や MOVLHPS (_mm_movelh_ps) 、下位が不要の場合は PSLLDQ (_mm_slli_si128) でも可能だが、 SSE（基本 2 オペランド）でソースとディスティネーションのレジスターが異なる（引数をまだ使う）場合は PSHUFD (_mm_shuffle_epi32) の方が有利。

	#define	DUPLO	0x44
	__m128i PP = _mm_shuffle_epi32(OP, DUPLO);

64 ビットの上位レーンと下位レーンの OR を、上位レーンと下位レーンの両方にコピーして入れたい場合、上位と下位を入れ替えて OR すればよい。

	flip2 = _mm_or_si128(flip2, _mm_shuffle_epi32(flip2, 0x4e));	// SWAP64

32 ビット 4 並列で実行する場合、64 ビット× 2 から 32 ビット× 4 にはもちろん PSHUFD が使えるが、64 ビット× 2 に戻す時も、ビットの重複がないので、下位を複製して xor することで上位の or と下位のクリアを同時に行える。

	// from C4/D4/E4/F4 toward LSB
	OL = _mm_shuffle_epi32(OP, 0xaa);
	PL = _mm_shuffle_epi32(OP, 0x00);
	outflankL = _mm_and_si128(MS1B_epu31(_mm_andnot_si128(OL, maskL)), PL);
	flippedL = _mm_and_si128(_mm_sub_epi32(_mm_setzero_si128(), _mm_add_epi32(outflankL, outflankL)), maskL);
	flipped = _mm_xor_si128(flippedL, _mm_shuffle_epi32(flippedL, 0xf5));

SSE2 実装の留意点

CPU では即値の演算が 64 ビット定数を除き一命令でできるが、SSE2 ではメモリー上の定数との演算になり、一命令でも 2 マイクロコードになる。命令数が同じなら、マスクを掛ける代わりにレジスターの縁を使いシフトでビットを切った方が有利な場合も。

	// H5 to A5
	outflank_h = _mm_and_si128(MS1B_epu31(_mm_andnot_si128(OO, _mm_set_epi32(0, 0, 0x0000007f, 0))), PP);
	// flipped = _mm_or_si128(flipped, _mm_and_si128(_mm_mullo_epi16(outflank_h, _mm_set1_epi16(-2)), _mm_set1_epi8(0x7e)));
	flipped = _mm_or_si128(flipped, _mm_srli_epi16(_mm_mullo_epi16(outflank_h, _mm_set_epi16(0, 0, 0, 0, 0, -0x0400, 0, 0)), 9));

0 と掛けるレーンは何でもいいので、メモリーとキャッシュを節約するため、他のレーンを使う定数と共用できることがある。
ただしサブルーチン内での定数の共用には落とし穴がある。一般には共用してレジスターに確保した方がいいのだが、そのためにスクラッチレジスターが不足して退避が必要になる場合がある。退避が必要になるくらいならレジスターに確保しない方がよいので、あえて別の定数にした方がいい場合がある（コンパイルしたコードを見ないとわからない）。
本当はコンパイラに正しく判断してほしいところだが、2018年時点では gcc でも clang でも msvc でもこの種の問題に遭遇することがある。 _mm_setzero_si128() によるゼロさえ複数回使うと、退避した上でレジスターに確保する場合があるので要注意。

AMD の CPU では整数と FP/SSE でパイプラインが分かれているので、CPU レジスターと SSE レジスターの間の転送は Intel に比べてコストがかかる。短い処理は汎用レジスターで処理した方が速いこともある。

vectorcall

Move generator が SSE/AVX になると、繰り返し呼ばれるので msvc, clang, icc でサポートされている vectorcall は効果がある。 x64 の vectorcall では第 5, 6 引数は vector の場合のみレジスター渡しになるので、整数型引数を第 4 引数までに納めるとよい。
gcc は linux では XMM/YMM でパラメータが渡されることがあるが、MinGW ではスタック渡しになってしまい、最適化能力が少し劣る msvc との性能差がかなり詰まる。

Flip AVX2 - AVX2 で返る石を求める

AVX2 (PP sequencial)

AVX2 では 8 方向 (4 方向× 2) の Flip が pos による場合分けのないすっきりした実装で可能になった。
隅や辺でも 8 方向計算することになるが、間接コールがなくなり、インライン化の可能性も出てくる。
左方向は LS1B または Carry propagaton が最善と思われるが、右方向はいくつかの候補を比較してみる。

右方向に Variable shift と Parallel Prefix を利用した例:

__m128i vectorcall mm_Flip(const __m128i OP, int pos)
{
	__m256i	PP, mOO, flip, shift2, pre, outflank, mask, ocontig;
	__m128i	flip2;
	const __m256i shift1897 = _mm256_set_epi64x(7, 9, 8, 1);

	PP = _mm256_broadcastq_epi64(OP);
	mOO = _mm256_and_si256(_mm256_permute4x64_epi64(_mm256_castsi128_si256(OP), 0x55),
		_mm256_set_epi64x(0x007e7e7e7e7e7e00, 0x007e7e7e7e7e7e00, 0x00ffffffffffff00, 0x7e7e7e7e7e7e7e7e));	// (sentinel on the edge)

	ocontig = _mm256_set1_epi64x(X_TO_BIT[pos]);
	ocontig = _mm256_and_si256(mOO, _mm256_srlv_epi64(ocontig, shift1897));
	ocontig = _mm256_or_si256(ocontig, _mm256_and_si256(mOO, _mm256_srlv_epi64(ocontig, shift1897)));
	pre = _mm256_and_si256(mOO, _mm256_srlv_epi64(mOO, shift1897));	// parallel prefix
	shift2 = _mm256_add_epi64(shift1897, shift1897);
	ocontig = _mm256_or_si256(ocontig, _mm256_and_si256(pre, _mm256_srlv_epi64(ocontig, shift2)));
	ocontig = _mm256_or_si256(ocontig, _mm256_and_si256(pre, _mm256_srlv_epi64(ocontig, shift2)));
	outflank = _mm256_and_si256(_mm256_srlv_epi64(ocontig, shift1897), PP);
	flip = _mm256_andnot_si256(_mm256_cmpeq_epi64(outflank, _mm256_setzero_si256()), ocontig);

	mask = lmask_v4[pos].v4;
		// look for non-opponent (or edge) bit
	ocontig = _mm256_andnot_si256(mOO, mask);
	ocontig = _mm256_and_si256(ocontig, _mm256_sub_epi64(_mm256_setzero_si256(), ocontig));	// LS1B
	outflank = _mm256_and_si256(ocontig, PP);
		// set all bits lower than outflank (depends on ocontig != 0)
	outflank = _mm256_add_epi64(outflank, _mm256_cmpeq_epi64(outflank, ocontig));
	flip = _mm256_or_si256(flip, _mm256_and_si256(outflank, mask));

	flip2 = _mm_or_si128(_mm256_castsi256_si128(flip), _mm256_extracti128_si256(flip, 1));
	flip2 = _mm_or_si128(flip2, _mm_shuffle_epi32(flip2, 0x4e));	// SWAP64

	return flip2;
}

ここで lmask_v4 は

const V4DI lmask_v4[66] = {
	{{ 0x00000000000000fe, 0x0101010101010100, 0x8040201008040200, 0x0000000000000000 }},	// a1
	{{ 0x00000000000000fc, 0x0202020202020200, 0x0080402010080400, 0x0000000000000100 }},	// b1
	{{ 0x00000000000000f8, 0x0404040404040400, 0x0000804020100800, 0x0000000000010200 }},	// c1

のような４方向へのビットマスク。
左方向で ocontig == 0 の時は outflank == ocontig が 0 == 0 となり誤った結果になるので、 ocontig が 0 にならないよう、O は（右方向と同様に）辺をマスクアウトしておく必要がある。

AVX2 (CVTPD2PS)

右方向が浮動小数変換による MS1B, 左方向は同じく LS1B だが番兵を使わない実装例。
AVX には PCMPEQQ はあるが PCMPNEQ はない。しかも NOT や NEG も一命令ではできない。そのため左方向のマスクも反転して消去するビットを 1 で持つようにする。
命令数は少ないが速度は振るわない。 AVX2 の浮動小数命令を利用すると、ライセンスベース†で AVX ベース周波数へのクロックダウンが起こることがあるようだ。

__m128i vectorcall mm_Flip(const __m128i OP, int pos)
{
	__m256i	PP, OO, flip, outflank, mask;
	__m128i	flip2;
	const __m256 exp_mask = _mm256_castsi256_ps(_mm256_set1_epi32(0xff800000));

	PP = _mm256_broadcastq_epi64(OP);
	OO = _mm256_permute4x64_epi64(_mm256_castsi128_si256(OP), 0x55);

	mask = rmask_v4[pos].v4;
		// look for non-opponent MS1B
	outflank = _mm256_andnot_si256(OO, mask);
		// MS1B_31 - clear mantissa to leave implicit MSB alone
	outflank = _mm256_cvtps_epi32(_mm256_and_ps(_mm256_cvtepi32_ps(outflank), exp_mask));
		// MS1B_32 - clear except sign bit if negative
	outflank = _mm256_andnot_si256(_mm256_srli_epi32(_mm256_srai_epi32(outflank, 31), 1), outflank);
		// MS1B_64 - clear low dword if high != 0
	outflank = _mm256_and_si256(outflank, _mm256_cmpeq_epi32(_mm256_srli_epi64(outflank, 32), _mm256_setzero_si256()));
	outflank = _mm256_and_si256(outflank, PP);
		// set all bits higher than outflank
	flip = _mm256_and_si256(_mm256_sub_epi64(_mm256_setzero_si256(), _mm256_add_epi64(outflank, outflank)), mask);

	mask = lmask_v4[pos].v4;
		// look for non-opponent LS1B
	outflank = _mm256_andnot_si256(OO, mask);
	outflank = _mm256_and_si256(outflank, _mm256_sub_epi64(_mm256_setzero_si256(), outflank));	// LS1B
	outflank = _mm256_and_si256(outflank, PP);
		// set all bits if outflank = 0, otherwise higher bits than outflank
	outflank = _mm256_sub_epi64(_mm256_cmpeq_epi64(outflank, _mm256_setzero_si256()), outflank);
	flip = _mm256_or_si256(flip, _mm256_andnot_si256(outflank, mask));

	flip2 = _mm_or_si128(_mm256_castsi256_si128(flip), _mm256_extracti128_si256(flip, 1));
	flip2 = _mm_or_si128(flip2, _mm_shuffle_epi32(flip2, 0x4e));	// SWAP64

	return flip2;
}

AVX2 (PSHUFB, LZCNT)

LS1B の方が計算量が少ないので、PSHUFB で上下反転し、LS1B で MS1B を求める例。 -1 方向のみ反転できないので、CPU の LZCNT を使うが、YMM には VPINSRQ できないので、VMOVQ と VPBLENDD で戻す。

__m128i vectorcall mm_Flip(const __m128i OP, int pos)
{
	__m256i	PP, mOO, flip, outflank, mask, ocontig, mbswapll;
	__m128i	flip2, outflank1;
	const __m256i mbswapll = _mm256_broadcastsi128_si256(_mm_set_epi64x(0x08090a0b0c0d0e0f, 0x0001020304050607));

	PP = _mm256_broadcastq_epi64(_mm_cvtsi64_si128(P));
	mOO = _mm256_and_si256(_mm256_permute4x64_epi64(_mm256_castsi128_si256(OP), 0x55),
		_mm256_set_epi64x(0x007e7e7e7e7e7e00, 0x007e7e7e7e7e7e00, 0x00ffffffffffff00, 0x7e7e7e7e7e7e7e7e));	// (sentinel on the edge)

	mask = rmask_v4[pos].v4;
	ocontig = _mm256_andnot_si256(mOO, mask);
		// -1 (CPU)
	outflank1 = _mm_cvtsi64_si128(0x8000000000000000ULL >> lzcnt_u64(_mm_cvtsi128_si64(_mm256_castsi256_si128(ocontig))));
		// -8/-7/-9 (bswap-LS1B)
	outflank = _mm256_shuffle_epi8(ocontig, mbswapll);
	outflank = _mm256_shuffle_epi8(_mm256_and_si256(outflank, _mm256_sub_epi64(_mm256_setzero_si256(), outflank)), mbswapll);	// LS1B
	outflank = _mm256_blend_epi32(outflank, _mm256_castsi128_si256(outflank1), 0x03);
	outflank = _mm256_and_si256(outflank, PP);
		// set all bits higher than outflank
	flip = _mm256_and_si256(_mm256_sub_epi64(_mm256_setzero_si256(), _mm256_add_epi64(outflank, outflank)), mask);

以下左方向は AVX2 (PP Seq) と同じ。

AVX2 (PSHUFB, PMAXUB)

PSHUFB による表引きで 4 ビットの、さらに PMAXUB で 8 ビットの MS1B を求め、上半分が 0 以外のときに下半分クリアを繰り返し、最上位バイトのみ残す例。

__m128i vectorcall mm_Flip(const __m128i OP, int pos)
{
	__m256i	PP, OO, flip, outflank, eraser, mask;
	__m128i	flip2;
	const __m256i mask0F0F = _mm256_set1_epi16(0x0F0F);
	const __m256i ms1bL = _mm256_broadcastsi128_si256(_mm_set_epi64x(0x0808080808080808, 0x0404040402020100));

	PP = _mm256_broadcastq_epi64(OP);
	OO = _mm256_permute4x64_epi64(_mm256_castsi128_si256(OP), 0x55);

	mask = rmask_v4[pos].v4;
		// look for non-opponent MS1B
	outflank = _mm256_andnot_si256(OO, mask);
		// mask to clear low half if high half != 0 in word/dword/qword
	eraser = _mm256_and_si256(_mm256_and_si256(
		_mm256_cmpeq_epi8(_mm256_srli_epi16(outflank, 8), _mm256_setzero_si256()),
		_mm256_cmpeq_epi16(_mm256_srli_epi32(outflank, 16), _mm256_setzero_si256())),
		_mm256_cmpeq_epi32(_mm256_srli_epi64(outflank, 32), _mm256_setzero_si256()));
		// table look up with PSHUFB then take MS1B of a byte with PMAXUB
	outflank = _mm256_max_epu8(_mm256_shuffle_epi8(ms1bL, _mm256_and_si256(outflank, mask0F0F)),
		_mm256_shuffle_epi8(_mm256_slli_epi64(ms1bL, 4), _mm256_and_si256(_mm256_srli_epi64(outflank, 4), mask0F0F)));
	outflank = _mm256_and_si256(_mm256_and_si256(outflank, eraser), PP);
		// set all bits higher than outflank
	flip = _mm256_and_si256(_mm256_sub_epi64(_mm256_setzero_si256(), _mm256_add_epi64(outflank, outflank)), mask);

AVX2 (PP fill)

Parallel Prefix Fill† により最上位の 1 以下のビットを全て立ててから 1 ビットずらして消し、MS1B を求める例。
見方を変えると、線上の P のうち ~O の最上位より下の影になっているビットを消して outflank を求めているとも言える。

__m128i vectorcall mm_Flip(const __m128i OP, int pos)
{
	__m256i	PP, OO, flip, outflank, eraser, mask;
	__m128i	flip2;

	PP = _mm256_broadcastq_epi64(OP);
	OO = _mm256_permute4x64_epi64(_mm256_castsi128_si256(OP), 0x55);

	mask = rmask_v4[pos].v4;
		// isolate non-opponent MS1B by clearing lower shadow bits
	eraser = _mm256_andnot_si256(OO, mask);
		// blute force parallel prefix fill
	outflank = _mm256_and_si256(PP, mask);
	eraser = _mm256_or_si256(eraser, _mm256_srli_epi64(eraser, 1));
	eraser = _mm256_or_si256(eraser, _mm256_srli_epi64(eraser, 2));
	eraser = _mm256_or_si256(eraser, _mm256_srli_epi64(eraser, 4));
	eraser = _mm256_or_si256(eraser, _mm256_srli_epi64(eraser, 8));
	eraser = _mm256_or_si256(eraser, _mm256_srli_epi64(eraser, 16));
	eraser = _mm256_or_si256(eraser, _mm256_srli_epi64(eraser, 32));
	outflank = _mm256_andnot_si256(eraser, _mm256_add_epi64(outflank, outflank));
		// set mask bits higher than outflank
	flip = _mm256_and_si256(mask, _mm256_sub_epi64(_mm256_setzero_si256(), outflank));

AVX2 (smart clr)

上記 Parallel prefix fill の部分は、variable shift により有効なビットだけを消去するようにもできる。
VPSRLVQ が VPSRLQ よりレイテンシーが大きい CPU もあるが、長い dependency chain になっている parallel prefix が 3 段少なくなる効果は大きい。

	outflank = _mm256_sllv_epi64(_mm256_and_si256(PP, mask), _mm256_set_epi64x(7, 9, 8, 1));
	eraser = _mm256_or_si256(eraser, _mm256_srlv_epi64(eraser, _mm256_set_epi64x(7, 9, 8, 1)));
	eraser = _mm256_or_si256(eraser, _mm256_srlv_epi64(eraser, _mm256_set_epi64x(14, 18, 16, 2)));
	eraser = _mm256_or_si256(eraser, _mm256_srlv_epi64(eraser, _mm256_set_epi64x(28, 36, 32, 4)));
	outflank = _mm256_andnot_si256(eraser, outflank);

AVX2 (PCMPGTQ)

マスクをかけた PP と空き = ~OO ^ PP を比較すると、O でない一番左のビット (O が切れた反対側のビット) が P か空きかを判断できるので、P の場合のみ flip を適用する。 acepck 氏のアイデア。MSB が立つことはないので、符号付き比較で符号なし比較を代用できる。
ステップ数は短いが、PCMPGTQ のレイテンシーが大きい CPU が多く、実行時間では劣る場合がある。

		// shadow mask lower than leftmost P
	rP = _mm256_and_si256(PP, mask);
	rS = _mm256_or_si256(rP, _mm256_srlv_epi64(rP, _mm256_set_epi64x(7, 9, 8, 1)));
	rS = _mm256_or_si256(rS, _mm256_srlv_epi64(rS, _mm256_set_epi64x(14, 18, 16, 2)));
	rS = _mm256_or_si256(rS, _mm256_srlv_epi64(rS, _mm256_set_epi64x(28, 36, 32, 4)));
		// apply flip if leftmost non-opponent is P
	rE = _mm256_xor_si256(_mm256_andnot_si256(OO, mask), rP);	// masked Empty
	flip = _mm256_and_si256(_mm256_andnot_si256(rS, mask), _mm256_cmpgt_epi64(rP, rE));

AVX512CD/VL (VPLZCNTQ)

レジスターは YMM (256bit) のまま (AVX512VL) だが、AVX512CD でついに追加された VPLZCNTQ (_mm256_lzcnt_epi64) を使う例。 (ただしライセンスベースのクロックダウンでは VPLZCNTQ は Heavy 扱い。)
AVX512 は近年の intel の一般向け CPU では削除されているものが多いが、256bit なので将来の AVX10† にも対応できるはず。
ternary logic は３項の任意のビット演算を真理値表により定義できる命令で、２つのビット演算が続くところを１命令にまとめられる。 ICC は当初から、MSVC も 2022 あたりからコンパイラがこの最適化を行うようになり、可読性の低い ternary logic を手書きする必要はなくなった (コメントアウトされている書き方でよい)。
64ビットの VPMINUQ (_mm256_min_epu64) も AVX512 で追加された命令。

__m128i vectorcall mm_Flip(const __m128i OP, int pos)
{
	__m256i	PP, OO, flip, outflank, mask;
	__m128i	flip2;

	PP = _mm256_broadcastq_epi64(OP);
	OO = _mm256_permute4x64_epi64(_mm256_castsi128_si256(OP), 0x55);

	mask = rmask_v4[pos];
		// right: look for non-opponent (or edge) bit with lzcnt
	outflank = _mm256_lzcnt_epi64(_mm256_andnot_si256(OO, mask));
	outflank = _mm256_and_si256(_mm256_srlv_epi64(_mm256_set1_epi64x(0x8000000000000000), outflank), PP);
		// clear masked OO lower than outflank
	// flip = _mm256_and_si256(_mm256_sub_epi64(_mm256_setzero_si256(), outflank), _mm256_and_si256(OO, mask));
	flip = _mm256_ternarylogic_epi64(_mm256_sub_epi64(_mm256_setzero_si256(), outflank), OO, mask, 0x80);

	mask = lmask_v4[pos];
		// left: look for non-opponent LS1B
	outflank = _mm256_andnot_si256(OO, mask);
	// outflank = _mm256_and_si256(outflank, _mm256_sub_epi64(_mm256_setzero_si256(), outflank));	// LS1B
	// outflank = _mm256_and_si256(outflank, PP);
	outflank = _mm256_ternarylogic_epi64(_mm256_sub_epi64(_mm256_setzero_si256(), outflank), outflank, PP, 0x80);
		// set all bits lower than outflank if outflank != 0
	outflank = _mm256_sub_epi64(outflank, _mm256_min_epu64(outflank, _mm256_set1_epi64x(1)));
	// flip = _mm256_or_si256(flip, _mm256_and_si256(outflank, mask));
	flip = _mm256_ternarylogic_epi64(flip, outflank, mask, 0xf8);

	flip2 = _mm_or_si128(_mm256_castsi256_si128(flip), _mm256_extracti128_si256(flip, 1));
	flip2 = _mm_or_si128(flip2, _mm_shuffle_epi32(flip2, 0x4e));	// SWAP64

	return flip2;
}

AVX512CD/VL (マスクレジスタ)

AVX2 は比較命令が少ないためにトリックが必要な場合があったが、AVX512 ではマスクレジスタが導入され、条件判断も結果の適用（条件付き実行）も柔軟になった。
右方向は acepck 氏の PCMPGTQ による方法、左方向は LS1B を含むそれより右のビット BLSMSK = x ^ (x - 1) により返る石を求めるとともに、それに P が含まれるか ( = LS1B が P か) で挟まれたかどうかを判定し、flip に加える。

		// right: look for player (or edge) bit with lzcnt
	__m256i	rM = rmask_v4[pos];
	__m256i	rP = _mm256_and_si256(PP, rM);
		// shadow mask lower than leftmost P
	__m256i	t0 = _mm256_srlv_epi64(_mm256_set1_epi64x(-1), _mm256_lzcnt_epi64(rP));
		// apply flip if leftmost non-opponent is P
	// __m256i rE = _mm256_andnot_si256(OO, _mm256_andnot_si256(rP, rM));
	__m256i	rE = _mm256_ternarylogic_epi64(OO, rM, rP, 0x04);	// masked empty
	__m256i rF = _mm256_maskz_andnot_epi64(_mm256_cmpgt_epi64_mask(rP, rE), t0, rM);

		// left: look for non-opponent LS1B
	__m256i	lM = lmask_v4[pos];
	__m256i	lO = _mm256_andnot_si256(OO, lM);
	// __m256i t2 = _mm256_xor_si256(_mm256_add_epi64(lO, _mm256_set1_epi64x(-1)), lO);	// BLSMSK
	// t2 = _mm256_and_si256(lM, t2);	// non-opponent LS1B and opponent inbetween
	__m256i	t2 = _mm256_ternarylogic_epi64(lM, _mm256_add_epi64(lO, _mm256_set1_epi64x(-1)), lO, 0x60);
		// apply flip if P is in mask, i.e. LS1B is P
	// __m256i flip = _mm256_mask_or_epi64(rF, _mm256_test_epi64_mask(PP, t2), rF, _mm256_andnot_si256(PP, t2));
	__m256i flip = _mm256_mask_ternarylogic_epi64(rF, _mm256_test_epi64_mask(PP, t2), PP, t2, 0xf2);

右方向も O が切れた位置を含むマスクを作ると、左右共通の処理を 512bit で処理することもできるが、準備や後処理もありあまりメリットはなさそうだ。

	mask = lrmask_v8[pos];
	outflank = _mm512_andnot_si512(OO, mask);
		// right: look for non-opponent (or edge) bit with lzcnt
	rmask = _mm512_extracti64x4_epi64(outflank, 1);
	rmask = _mm256_srav_epi64(_mm256_set1_epi64x(0x8000000000000000), _mm256_lzcnt_epi64(rmask));
		// left: look for non-opponent LS1B
	lmask = _mm512_castsi512_si256(outflank);
	lmask = _mm256_xor_si256(lmask, _mm256_add_epi64(lmask, _mm256_set1_epi64x(-1)));	// BLSMSK
		// outflank and opponent inbetween
	mask = _mm512_and_si512(mask, _mm512_inserti64x4(_mm512_castsi256_si512(lmask), rmask, 1));
		// apply flip if P is in mask, i.e. outflank is P
	flip = _mm512_maskz_and_epi64(_mm512_test_epi64_mask(mask, PP), mask, OO);

Move Generator ベンチマーク

intel i7-4790 (Haswell), Windows 10 での実行時間
(Haswell で実行できない AVX512 を除く)

	fforum-20-39 1-thread (sec)			fforum-40-59 8-threads (m:ss)
	gcc 5.1	vc 2019	clang 6	gcc 5.1	vc 2019	clang 6
AVX2 (smart clr)	2.972	2.982	3.139	2:35.0	2:36.3	2:41.8
AVX2 (PP seq)	3.000	3.034	3.220	2:35.4	2:39.0	2:49.9
AVX2 (LZCNT)	3.062	3.029	3.105	2:34.5	2:40.2	2:47.6
AVX2 (PP fill)	3.111	2.999	3.143	2:37.5	2:39.0	2:47.6
AVX2 (CVTPD2PS)	3.454	3.373	3.470	2:46.5	2:53.8	2:55.5
SSE2	3.107	3.152	3.311	2:39.7	2:47.6	2:55.2
carry+LZCNT	3.126	3.221	3.376	2:53.1	3:02.4	3:03.2
carry propagation	3.235	3.266	3.512	2:52.4	2:58.6	3:13.5
kindergarten	3.361	3.440	3.515	3:02.9	3:06.9	3:11.7

Flip Neon - Arm Neon / SVE で返る石を求める

Arm Neon (vclz)

Arm Neon は 128 ビットだが、vclz と可変シフトが使える。ただし vclz は 32x4 までなので、上位が 0 のときのみ下位に MSB を作り MS1B を 64 ビット化する。
また Neon では 64 ビットの飽和減算(qsub) が可能で、Outflank = 0 のとき足し戻す処理が不要になる。
vbsl (bitwise select) は and-or を置き換えるのに使える。

#ifndef __aarch64__
#define vceqzq_u32(x)	vmvnq_u32(vtstq_u32((x), (x)))
#define	vnegq_s64(x)	vsubq_s64(vdupq_n_s64(0), (x))
#endif

uint64_t Flip(int pos, uint64_t P, uint64_t O)
{
	uint64x2_t	flip, oflank0, mask0;				uint64x2_t	oflank1, mask1;
	int32x4_t	clz0;						int32x4_t	clz1;
	uint32x4_t	msb0;						uint32x4_t	msb1;
	const uint64x2_t one = vdupq_n_u64(1);
	uint64x2_t PP = vdupq_n_u64(P);
	uint64x2_t OO = vdupq_n_u64(O);

	mask0 = lrmask_v4[pos][2];					mask1 = lrmask_v4[pos][3];
		// isolate non-opponent MS1B
	oflank0 = vbicq_u64(mask0, OO);					oflank1 = vbicq_u64(mask1, OO);
		// outflank = (0x8000000000000000ULL >> lzcnt) & P
	clz0 = vclzq_s32(vreinterpretq_s32_u64(oflank0));		clz1 = vclzq_s32(vreinterpretq_s32_u64(oflank1));
		// set loword's MSB if hiword = 0
	msb0 = vreinterpretq_u32_u64(vshrq_n_u64(oflank0, 32));		msb1 = vreinterpretq_u32_u64(vshrq_n_u64(oflank1, 32));
	msb0 = vshlq_n_u32(vceqzq_u32(msb0), 31);			msb1 = vshlq_n_u32(vceqzq_u32(msb1), 31);
	msb0 = vshlq_u32(msb0, vnegq_s32(clz0));			msb1 = vshlq_u32(msb1, vnegq_s32(clz1));
	oflank0 = vandq_u64(vreinterpretq_u64_u32(msb0), PP);		oflank1 = vandq_u64(vreinterpretq_u64_u32(msb1), PP);
		// set all bits higher than outflank
	oflank0 = vreinterpretq_u64_s64(vnegq_s64(vreinterpretq_s64_u64(oflank0)));
	oflank1 = vreinterpretq_u64_s64(vnegq_s64(vreinterpretq_s64_u64(oflank1)));
	flip = vandq_u64(vbslq_u64(mask1, oflank1, vandq_u64(mask0, oflank0)), OO);

	mask0 = lrmask_v4[pos][0];					mask1 = lrmask_v4[pos][1];
		// get outflank with carry-propagation
	oflank0 = vaddq_u64(vornq_u64(OO, mask0), one);			oflank1 = vaddq_u64(vornq_u64(OO, mask1), one);
	oflank0 = vandq_u64(vandq_u64(PP, mask0), oflank0);		oflank1 = vandq_u64(vandq_u64(PP, mask1), oflank1);
		// set all bits lower than oflank, using satulation if oflank = 0
	oflank0 = vqsubq_u64(oflank0, one);				oflank1 = vqsubq_u64(oflank1, one);
	flip = vbslq_u64(mask1, oflank1, vbslq_u64(mask0, oflank0, flip));

	return vget_lane_u64(vorr_u64(vget_low_u64(flip), vget_high_u64(flip)), 0);
}

Arm Neon (rbit)

aarch64 のみだが Neon で rbit が使えるので、左右方向で 6 命令以上違う場合は、全方向について重い方を逆方向に置換できる。

uint64x2_t mm_Flip(uint64x2_t OP, int pos)
{
	uint64x2_t	flip, oflank0, mask0, oflank1, mask1;
	const uint64x2_t one = vdupq_n_u64(1);
	uint64x2_t rOP = vreinterpretq_u64_u8(vrev64q_u8(vrbitq_u8(vreinterpretq_u8_u64(OP))));
	uint64x2_t PP = vdupq_lane_u64(vget_low_u64(OP), 0);	uint64x2_t rPP = vdupq_lane_u64(vget_low_u64(rOP), 0);
	uint64x2_t OO = vdupq_lane_u64(vget_high_u64(OP), 0);	uint64x2_t rOO = vdupq_lane_u64(vget_high_u64(rOP), 0);

	mask0 = lrmask_v4[pos][2];				mask1 = lrmask_v4[pos][3];
		// get outflank with carry-propagation
	oflank0 = vaddq_u64(vornq_u64(rOO, mask0), one);	oflank1 = vaddq_u64(vornq_u64(rOO, mask1), one);
	oflank0 = vandq_u64(vandq_u64(rPP, mask0), oflank0);	oflank1 = vandq_u64(vandq_u64(rPP, mask1), oflank1);
		// set all bits lower than oflank, using satulation if oflank = 0
	oflank0 = vqsubq_u64(oflank0, one);			oflank1 = vqsubq_u64(oflank1, one);
	flip = vbslq_u64(mask1, oflank1, vandq_u64(mask0, oflank0));
	flip = vreinterpretq_u64_u8(vrev64q_u8(vrbitq_u8(vreinterpretq_u8_u64(flip))));

	mask0 = lrmask_v4[pos][0];				mask1 = lrmask_v4[pos][1];
		// get outflank with carry-propagation
	oflank0 = vaddq_u64(vornq_u64(OO, mask0), one);		oflank1 = vaddq_u64(vornq_u64(OO, mask1), one);
	oflank0 = vandq_u64(vandq_u64(PP, mask0), oflank0);	oflank1 = vandq_u64(vandq_u64(PP, mask1), oflank1);
		// set all bits lower than oflank, using satulation if oflank = 0
	oflank0 = vqsubq_u64(oflank0, one);			oflank1 = vqsubq_u64(oflank1, one);
	flip = vbslq_u64(mask1, oflank1, vbslq_u64(mask0, oflank0, flip));

	return vorrq_u64(flip, vextq_u64(flip, flip, 1));
}

Arm SVE (svclz)

デフォルトでコンパイルするとスケーラブルなコードに、sve-vector-bits を指定してコンパイルすると条件分岐のないコードになる。
SVE128 を Neon と比較すると、svclz が 64ビットに対応し、スカラー値オペランドの追加などもあるが、プレディケーションによるコードの増加や、 Neon では並べて書いていたコードがシリアライズされることもあり、ほとんどメリットは無いようだ。
SVE256 なら効率の良いコードになるが、2024 年時点では実装されている CPU は非常に少ない。

#ifndef __ARM_FEATURE_SVE2
	// equivalent only if no intersection between masks
#define svbsl_u64(op1,op2,op3)	svorr_u64_m(pg, (op2), svand_u64_x(pg, (op3), (op1)))
#endif

uint64_t Flip(int pos, uint64_t P, uint64_t O)
{
	svuint64_t	PP, OO, flip, oflank, mask, msb;
	svbool_t	pg;
	const uint64_t	(*pmask)[8];

	PP = svdup_u64(P);
	OO = svdup_u64(O);
	msb = svdup_u64(0x8000000000000000);
	pmask = &lrmask[pos];
	pg = svwhilelt_b64(0, 4);

	mask = svld1_u64(pg, *pmask + 4);
		// right: isolate non-opponent MS1B
	oflank = svbic_u64_x(pg, mask, OO);
		// outflank = (0x8000000000000000ULL >> lzcnt) & P
	oflank = svand_u64_x(pg, svlsr_u64_x(pg, msb, svclz_u64_x(pg, oflank)), PP);
		// set all bits higher than outflank
	oflank = svreinterpret_u64_s64(svneg_s64_x(pg, svreinterpret_s64_u64(oflank)));
	flip = svand_u64_x(pg, mask, oflank);

	mask = svld1_u64(pg, *pmask + 0);
		// left: look for non-opponent LS1B
	oflank = svbic_u64_x(pg, mask, OO);
	oflank = svand_u64_x(pg, svbic_u64_x(pg, oflank, svsub_n_u64_x(pg, oflank, 1)), PP);
		// set all bits lower than oflank, using satulation if oflank = 0
	flip = svbsl_u64(svqsub_n_u64(oflank, 1), flip, mask);

	if (svcntd() == 2) {	// sve128 only
		mask = svld1_u64(pg, *pmask + 6);
			// right: isolate non-opponent MS1B
		oflank = svbic_u64_x(pg, mask, OO);
			// outflank = (0x8000000000000000ULL >> lzcnt) & P
		oflank = svand_u64_x(pg, svlsr_u64_x(pg, msb, svclz_u64_x(pg, oflank)), PP);
			// set all bits higher than outflank
		oflank = svreinterpret_u64_s64(svneg_s64_x(pg, svreinterpret_s64_u64(oflank)));
  		flip = svbsl_u64(oflank, flip, mask);

		mask = svld1_u64(pg, *pmask + 2);
			// left: look for non-opponent LS1B
		oflank = svbic_u64_x(pg, mask, OO);
		oflank = svand_u64_x(pg, svbic_u64_x(pg, oflank, svsub_n_u64_x(pg, oflank, 1)), PP);
			// set all bits lower than oflank, using satulation if oflank = 0
		flip = svbsl_u64(svqsub_n_u64(oflank, 1), flip, mask);
	}

	return svorv_u64(pg, svand_u64_x(pg, flip, OO));
}

(番外) AVX2 によるチェスの Sliding Attack†

チェスの Queen, Rook, Bishop の移動範囲を求めるには通常 Magic Bitboards† (または PEXT Bitboards†) が使われるが、AVX2 を使うと大きなテーブルなしでそれに近い速度で求められる。リバーシの Flip に近いが、引数は敵味方の区別がない Occupied のみになる。
Intel では PEXT の方が早いが、AMD では Magic Bitboards よりわずかに速いこともある†ようだ。
FishTest での速度とクリーンなコードを重視する Stockfish には取り入れられないだろうが、 CFish†には pull してもらえ、 Chess Programming Wiki†にも取り上げてもらえた。

// avx2 version of BLSMSK (https://www.chessprogramming.org/BMI1#BLSMSK)
INLINE __m256i blsmsk64x4(__m256i y) {
  return _mm256_xor_si256(_mm256_add_epi64(y, _mm256_set1_epi64x(-1)), y);
}

INLINE Bitboard attacks_bb_queen(Square s, Bitboard occupied)
{
  const __m256i occupied4 = _mm256_set1_epi64x(occupied);
  const __m256i lmask = queen_mask_v4[s][0];
  const __m256i rmask = queen_mask_v4[s][1];
  __m256i slide4, rslide;
  __m128i slide2;

    // Left bits: set mask bits lower than occupied LS1B
  slide4 = _mm256_and_si256(occupied4, lmask);
  slide4 = _mm256_and_si256(blsmsk64x4(slide4), lmask);
    // Right bits: set shadow bits lower than occupied MS1B (6 bits max)
  rslide = _mm256_and_si256(occupied4, rmask);
  rslide = _mm256_or_si256(_mm256_srlv_epi64(rslide, _mm256_set_epi64x(14, 18, 16, 2)),  // PP Fill
    _mm256_srlv_epi64(rslide, _mm256_set_epi64x(7, 9, 8, 1)));
  rslide = _mm256_or_si256(_mm256_srlv_epi64(rslide, _mm256_set_epi64x(28, 36, 32, 4)),
    _mm256_or_si256(rslide, _mm256_srlv_epi64(rslide, _mm256_set_epi64x(14, 18, 16, 2))));
    // add mask bits higher than blocker
  slide4 = _mm256_or_si256(slide4, _mm256_andnot_si256(rslide, rmask));
    // OR 4 vectors
  slide2 = _mm_or_si128(_mm256_castsi256_si128(slide4), _mm256_extracti128_si256(slide4, 1));
  return _mm_cvtsi128_si64(_mm_or_si128(slide2, _mm_unpackhi_epi64(slide2, slide2)));
}

INLINE Bitboard attacks_bb_rook(Square s, Bitboard occupied) {
    // North bits: set mask bits lower than occupied LS1B
  Bitboard mask = 0x0101010101010100 << s;
  Bitboard slides = _blsmsk_u64(occupied & mask) & mask;

    // South bits: flip vertical to simulate MS1B by LS1B
  mask = 0x0101010101010100 << (s ^ 0x38);
  slides |= __builtin_bswap64(_blsmsk_u64(__builtin_bswap64(occupied) & mask) & mask);

    // East-West: from precomputed table
  int r8 = s & 0x38;
  slides |= (Bitboard)(rook_attacks_EW[((occupied >> r8) & 0x7e) * 4 + (s & 0x07)]) << r8;
  return slides;
}

INLINE Bitboard attacks_bb_bishop(Square s, Bitboard occupied)
{
    // flip vertical to simulate MS1B by LS1B
  const __m128i swapl2h = _mm_set_epi8(0, 1, 2, 3, 4, 5, 6, 7, 7, 6, 5, 4, 3, 2, 1, 0);
  __m128i occupied2 = _mm_shuffle_epi8(_mm_cvtsi64_si128(occupied), swapl2h);
  __m256i occupied4 = _mm256_broadcastsi128_si256(occupied2);

  const __m256i mask = bishop_mask_v4[s];
    // set mask bits lower than occupied LS1B
  __m256i slide4 = _mm256_and_si256(blsmsk64x4(_mm256_and_si256(occupied4, mask)), mask);

  __m128i slide2 = _mm_or_si128(_mm256_castsi256_si128(slide4), _mm256_extracti128_si256(slide4, 1));
  const __m128i swaph2l = _mm_set_epi8(15, 14, 13, 12, 11, 10, 9, 8, 8, 9, 10, 11, 12, 13, 14, 15);
  return _mm_cvtsi128_si64(_mm_or_si128(slide2, _mm_shuffle_epi8(slide2, swaph2l)));
}

リバーシのビットボード テクニック

Population count - 現時点の石数

Mirroring - 鏡像

1バイトの鏡像

PSHUFB(SSSE3) による鏡像

BSWAP による上下反転

AVX2 によるX-Y軸の入れ替え

Mobility - 着手可能位置

左横方向, CPU (キャリー伝播)

右横方向, SSE2 (飽和減算)

8 方向, SSE2 + CPU

8 方向, AVX2

8 方向, CPU

Get full lines - 埋まっている列を求める

横方向, CPU

横方向, SSE2

縦方向, CPU

斜め方向, CPU

斜め方向, SSE2

斜め方向, AVX2 (Kogge-Stone)

斜め方向, AVX2 (PCMPEQQ)

Count Last Flip - 最終手での返る石数

Kindergarten bitboard†

90°/ 135° merge

LS1B isolation† の利用

LZCNT, __builtin_clzll の利用

BMI2 (PEXT)

SSE2 (PMOVMSKB, PSADBW) (_mm_movemask_epi8, _mm_sad_epu8)

Arm Neon (vaddvq)

AVX512CD/VL (VPLZCNTQ)

Flip - 返る石を求める (Move Generator)

Outflank - Flip テーブル参照による方法

シフトの繰り返しによる方法

Parallel Prefix

キャリー伝播 (MSB 方向のみ)

LS1Bの利用 (MSB 方向のみ)

LZCNT (LSB 方向のみ)

__builtin_clzll (LSB 方向のみ)

浮動小数変換 (MS1B) (LSB 方向のみ)

Outflank → Flip (MSB方向)

Outflank → Flip (LSB方向)

飽和減算 (PSUBUSB) (_mm_subs_epu8)

PMULLW (_mm_mullo_epi16)

PMULHUW (_mm_mulhi_epu16), PMINSW (_mm_min_epi16)

PMINUB (_mm_min_epu8)

積和演算 (PMADDWD) (_mm_madd_epi16)

飽和加算 (PADDUSB) (_mm_adds_epu8)

PACKUSWB (_mm_packus_epi16)

SSE2 でのテーブル参照

PSHUFD (_mm_shuffle_epi32)

SSE2 実装の留意点

vectorcall

Flip AVX2 - AVX2 で返る石を求める

AVX2 (PP sequencial)

AVX2 (CVTPD2PS)

AVX2 (PSHUFB, LZCNT)

AVX2 (PSHUFB, PMAXUB)

AVX2 (PP fill)

AVX2 (smart clr)

AVX2 (PCMPGTQ)

AVX512CD/VL (VPLZCNTQ)

AVX512CD/VL (マスクレジスタ)

Move Generator ベンチマーク

Flip Neon - Arm Neon / SVE で返る石を求める

Arm Neon (vclz)

Arm Neon (rbit)

Arm SVE (svclz)

(番外) AVX2 によるチェスの Sliding Attack†

Edax AVX の Source Code†

Booby Reversi Home

リバーシのビットボードテクニック